Question

【题目】如图，在等边三角形ABC中，AD⊥BC于点D，以AD为一边向右作等边三角形ADE，DE与AC交于点F.

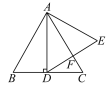
(1)试判断DF与EF的数量关系，并给出证明；

(2)若CF的长为2 cm，试求等边三角形ABC的边长．

Answer 1

【答案】(1)DF＝EF (2) 8cm

【解析】

(1)根据等边三角形的每一个角都是60°可得∠BAC=∠DAE=60°,再根据等腰三角形三线合一的性质求出BD=DC,∠BAD=∠DAC=30°,然后得到∠DAC=∠CAE,然后根据等腰三角形三线合一的性质即可得证;(2)求出∠CDF=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.

:(1)DF=EF.
理由: ∵△ABC和△ADE均是等边三角形,
∴∠BAC=∠DAE=60°,
∵AD⊥BC,
∴BD=DC,∠BAD=∠DAC=×60°=30°,
∴∠CAE=60°-30°=30°,
即∠DAC=∠CAE,
∴AC垂直平分DE,
∴DF=EF;
(2)在RT△DFC中, ∵∠FCD=60°, ∠CFD=90°,
∴∠CDF=90°-60°=30°,
∵CF=2cm,
∴DC=4cm,
∴BC=2DC=2×4=8cm,
即等边三角形ABC的边长为8cm.

(1)DF＝EF.证明：∵△ABC是等边三角形，∴∠BAC＝60°，又∵AD⊥BC，∴∠DAC＝30°.∵△ADE是等边三角形，∴∠DAE＝60°，∴∠DAF＝∠EAF＝30°，由三线合一知DF＝EF　(2)BC＝2CD＝2×2CF＝8 cm