题目内容
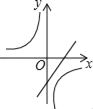
【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.

(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
【答案】(1)y=1.4x+2.8(2)7元(3)21元;(4)20km.
【解析】
(1)根据(3,7)、(8,14)利用待定系数法即可得到当x≥3时的函数关系式;
(2)根据图像直接得到;
(3)把x=13代入直线BC即可求解;
(4)令y=30.8,代入求出x即可.
(1)x≥3时,BC的直线解析式为y=kx+b,(k≠0)
把(3,7)、(8,14)代入得![]()
解得![]() ,∴BC的直线解析式为y=1.4x+2.8,
,∴BC的直线解析式为y=1.4x+2.8,
故x≥3时的函数关系式为y=1.4x+2.8,
(2)由图像可知,乘坐2.5km,应付7元;
(3)令x=13,代入y=1.4×13+2.8=21元;
(4)令y=30.8,代入30.8=1.4x+2.8,解得x=20km.

 优生乐园系列答案
优生乐园系列答案【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?