题目内容
【题目】如图,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边三角形ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;

【答案】BD存在最大值,最大值是6.
【解析】
以AD为边做作等边三角形ADE,连接CE,根据等边三角形的性质和全等三角形的判定证明△ABD≌△ACE,再利用全等三角形的性质以及两点之间线段最短,即可证得结论.
证明:BD存在最大值;
如图,以AD为边做作等边三角形ADE,连接CE,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE=DE=2,∠BAC=∠EAD=60°,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠EAD+∠DAC
∴∠BAD=∠EAC,且AB=AC,AD=AE
∴△ABD≌△ACE
∴BD=CE
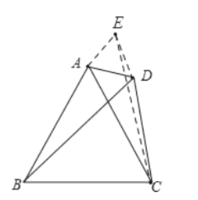
若点E,点D,点C不在一条直线上,则EC<ED+DC;
若点E,点D,点C在一条直线上,则EC=ED+DC.
∴EC≤ED+CD=2+4=6
∴BD≤6,
∴BD存在最大值,最大值是6.

练习册系列答案
相关题目