题目内容
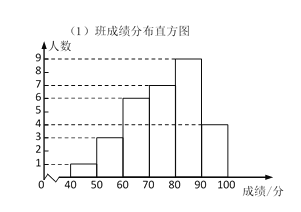
【题目】如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.
(问题发现)
(1)如图(2),当n=1时,BM与PD的数量关系为 ,CN与PD的数量关系为 .
(类比探究)
(2)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.
(拓展延伸)
(3)在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长

【答案】(1)BM=PD;![]() (2)见解析 (3)
(2)见解析 (3)![]() 或
或![]()
【解析】
(1)当n=1时四边形ABCD和四边形AMNP均为正方形,所以AM=AP,AB=AD,从而得出BM=PD,再根据![]() 得出
得出![]() ,从而得出结论;
,从而得出结论;
(2)连接AC,证明![]() ,即可求解;
,即可求解;
(3)分两种情况考虑:通过证![]() 得出对应边数量关系,设
得出对应边数量关系,设![]() ,则
,则![]() 解直角三角形AQM,从而计算出QM的长度,从而求算CN.
解直角三角形AQM,从而计算出QM的长度,从而求算CN.
(1)解:∵当n=1时四边形ABCD和四边形AMNP均为正方形
∴AM=AP,AB=AD
∴BM=PD
又∵![]()
∴![]()
∴![]()
(2)CN与PD之间的数量关系发生变化,![]() .
.
理由:连接AC,如图:

在矩形ABCD和矩形AMNP中,
∵.AD=2AB, AP=2AM,
∴![]() ,
,![]()
∴.![]()
易得![]()
∴△ANC∽△APD
∴![]()
∴![]()
(3)分两种情况考虑:
①如图:

∵已知AD=4,AP=2,![]()
∴AB=2,AM=PN=1
由图知:![]()
∴![]()
设![]() ,则
,则![]() ,在直角三角形AQM中:
,在直角三角形AQM中:![]()
解得:![]() (舍)
(舍)
∴![]() ,
,![]()
∴![]()
∴![]()
②如图:

由①可得:![]() ,
,![]() ,MN=2
,MN=2
∴![]()

 名校课堂系列答案
名校课堂系列答案【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?