题目内容
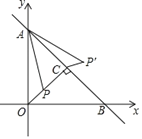
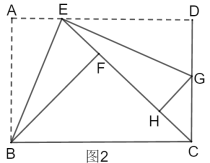
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() ,
,![]() 重合的一个动点,直线
重合的一个动点,直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,当
,当![]() 是直角三角形时,
是直角三角形时,![]() 的长为______.
的长为______.
【答案】2或![]()
【解析】
分两种情况讨论:
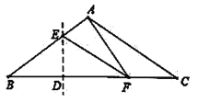
①当∠AFC=90°时,AF⊥BC,利用等腰三角形的三线合一性质和垂直平分线的性质可解;
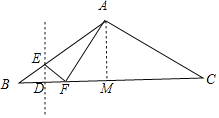
②当∠CAF=90°时,过点A作AM⊥BC于点M,证明△AMC∽△FAC,列比例式求出FC,从而得BF,再利用垂直平分线的性质得BD.
①当∠AFC=90°时,AF⊥BC,
∵AB=AC,
∴BF=![]() BC=4
BC=4
∵DE垂直平分BF,
∴BD=![]() BF=2;
BF=2;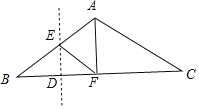
②当∠CAF=90°时,过点A作AM⊥BC于点M,
∵AB=AC,
∴BM=CM,
在Rt△AMC与Rt△FAC中,∠AMC=∠FAC=90°,∠C=∠C,
∴△AMC∽△FAC,
∴![]()
∵AC=10,MC=![]() BC=4,
BC=4,
∴![]()
∴BF=BC-FC=![]()
∴BD=![]() BF=
BF=![]() .
.
故答案为2或![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
个数 | 11 | 12 | 13 | 12 |
其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()