Question

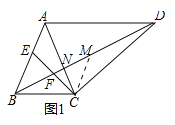
【题目】如图，四边形ABCD中，AD∥BC．

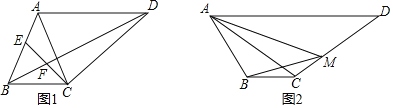
（1）如图1，AB＝AC，点E为AB上一点，∠BEC＝∠ACD．

①求证：ABBC＝ADBE；

②连接BD交CE于F，试探究CF与CE的数量关系，并证明；

（2）如图2，若AB≠AC，点M在CD上，cos∠DAC＝cos∠BMA＝，AC＝CD＝3MC，ADBC＝12，直接写出BC的长．

Answer 1

【答案】（1）①见解析，②CE＝2CF，见解析；（2）

【解析】

（1）①证明△BEC∽△ACD可得结论．

②结论：CE＝2CF．利用相似三角形的性质证明CM＝BE，再证明△MCF≌△BEF（ASA），推出CF＝EF即可解决问题．

（2）如图2中，作CH⊥AD于H．证明△ABC∽△AMD，可得ACDM＝BCAD＝12，由AC＝CD＝3CM，推出6CM2＝12，推出CM＝ ， ，解直角三角形求出AD即可解决问题．

（1）①∵AD∥BC，

∴∠DAC＝∠ACB，

∵AB＝AC，

∴∠ABC＝∠ACB，

∴∠ABC＝∠CAD，

∵∠BEC＝∠ACD，

∴△BEC∽△ACD，

∴，

∴BCAC＝ADBE，

∵AB＝AC，

∴ABBC＝ADBE．

②解：结论：CE＝2CF．

理由：如图1中，作CM∥AB交BD于M，设BD交AC于N．

∵CM∥AB，

∴∠BAN＝∠MCN，∠CMN=∠ABN，

∴△MCN∽△BAN，

∴，

∵AD∥BC，

∴∠NAD＝∠NCB，∠AND＝∠CNB，

∴△CNB∽△AND，

∴，

∵，

∴，

∵AB＝AC，

∴CM＝BE，

∵CM∥BE，

∴∠CMF＝∠BEF，∠BEF＝∠MCF，

∴△MCF≌△BEF（ASA），

∴CF＝EF，

∴CE＝2CF．

（2）解：如图2中，作CH⊥AD于H．

∵AD∥BC，

∴∠CAD＝∠ACB，

∵cos∠DAC＝cos∠BMA，

∴∠DAC＝∠AMB，

∴∠AMB＝∠ACB，

∴A，B，C，M四点共圆，

∴∠BAC＝∠BMC，

∵CA＝CD，

∴∠CAD＝∠D＝∠AMB，

∵∠AMC＝∠MAD+∠D＝∠BMA+∠BMC，

∴∠BMC＝∠MAD，

∴∠BAC＝∠MAD，

∵∠ACB＝∠AMB＝∠D，

∴△ABC∽△AMD，

∴，

∴ACDM＝BCAD＝12，

∵AC＝CD＝3CM，

∴6CM2＝12，

∵CM＞0，

∴CM＝，

∴，

∵CH⊥AD，

∴AH＝DH，

∵，

∴， ，

∵BCAD＝12，

∴．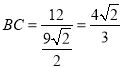