��Ŀ����
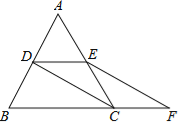
����Ŀ��һ�����ǰ���ͼ1�ڷ�,��C=��DFE=90,��B=30,��E=45,��F��BC��,��A��DF��,��AFƽ�֡�CAB,�ֽ����ǰ�DFE�Ƶ�F˳ʱ����ת(����D��������FB��ʱֹͣ��ת).
(1)����AFD=_ __ʱ,DF��AC;����AFD=__ _ʱ��DF��AB��
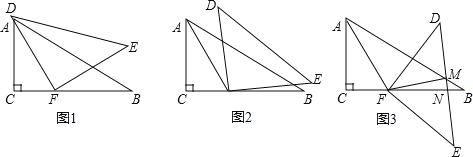
(2)����ת�����У�DF��AB�Ľ����ΪP����ͼ2����AFP�������ڽ���ȣ����APD�Ķ�����
(3)����DE���AB��BC�ֱ��ڵ�M��Nʱ����ͼ3������AFM=2��BMN���Ƚϡ�FMN���FNM�Ĵ�С����˵�����ɡ�
���𰸡�(1)30��60(2) 60��105��150(3)��FMN=��FNM
����������������1������AFD=30��ʱ��AC��DF�����ݽ�ƽ���ߵĶ��������á�CAF=��FAB=30�㣬���ڴ����������ֱ��ƽ������֤��AC��DF��������AFD=60��ʱ��DF��AB���������ε��ڽǺͶ���֤��������
��2����Ϊ��FAP=��AFP����AFP=��APF����APF=��FAP���������⼴����
��3����������������ǵ�����֤����FNM=30��+��BMN����������������������ǵ������Լ���AFM�͡�BMN�Ĺ�ϵ��֤����FMN=30��+��BMN���Ӷ��ɵõ���FNM���FMN�Ĺ�ϵ��
�������1����ͼ1��ʾ��

����AFD=30ʱ��AC��DF��
�������ߡ�CAB=60�㣬AFƽ�֡�CAB�����CAF=30�㣮
�ߡ�AFD=30�㣬���CAF=��AFD����AC��DF��
��ͼ2��ʾ������AFD=60��ʱ��DF��AB��
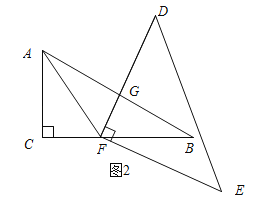
�ߡ�CAB=60�㣬AFƽ�֡�CAB�����AFG=30�㣮
�ߡ�AFD=60�㣬���FGB=90�㣬��DF��AB��
�ʴ�Ϊ��30��60��
��2���ߡ�CAB=60�㣬AFƽ�֡�CAB�����FAP=30�㣮
����ͼ3��ʾ��

����FAP=��AFP=30��ʱ����APD=��FAP+��AFP=30��+30��=60�㣻
��ͼ4��ʾ��

����AFP=��APFʱ��
�ߡ�FAP=30�㣬��AFP=��APF�����AFP=��APF=![]() ����180�㩁30�㣩=
����180�㩁30�㣩=![]() ��150��=75�㣬���APD=��FAP+��AFP=30��+75��=105�㣻
��150��=75�㣬���APD=��FAP+��AFP=30��+75��=105�㣻
��ͼ5��ʾ��
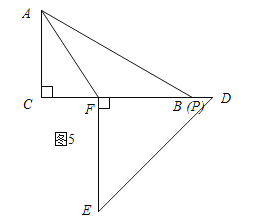
��ͼ5��ʾ������APF=��FAP=30��ʱ��
��APD=180�㩁30��=150�㣮
������������APD�Ķ���Ϊ60����105����150�㣮
��3����FMN=��FNM��
��������ͼ6��ʾ��
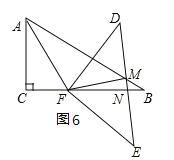
�ߡ�FNM�ǡ�BMN��һ����������FNM=��B+��BMN��
�ߡ�B=30�㣬���FNM=��B+��BMN=30��+��BMN��
�ߡ�BMF�ǡ�AFM��һ����������MBF=��MAF+��AFM������BMN+��FMN=��MAF+��AFM��
�֡ߡ�MAF=30�㣬��AFM=2��BMN�����BMN+��FMN=30��+2��BMN�����FMN=30��+��BMN�����FNM=��FMN��

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�