题目内容
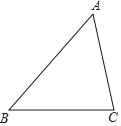
【题目】如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，DC=12，AD=13，求四边形ABCD的面积．
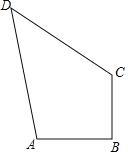
【答案】四边形ABCD的面积为36.
【解析】
连接AC，然后根据勾股定理求出AC的长度，再根据勾股定理逆定理计算出∠ACD=90°，然后根据四边形ABCD的面积=△ABC的面积+△ACD的面积，列式进行计算即可得解．
连接AC，
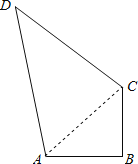
∵∠ABC=90°，AB=3，BC=4，
∴AC=
=5，
∵DC=12，AD=13，
∴AC2+DC2=52+122=25+144=169，
AD2=132=169，
∴AC2+DC2=AD2，
∴△ACD是∠ACD=90°的直角三角形，
四边形ABCD的面积=△ABC的面积+△ACD的面积，
=
ABBC+ACCD
=×3×4+×5×12
=6+30
=36．
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
【题目】某自行车厂一周计划生产150辆自行车，平均每天生产辆，由于各种原因实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产为正、减产为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
（1）根据记录可知前三天共生产 辆；
（2）产量最多的一天比生产量最少的一天多生产 辆；
（3）该厂实行计划工资制，每辆车
元，超额完成任务每辆奖
元，少生产一辆扣元，那么该厂工人这一周的工资总额是多少？
【题目】小明家2002年四个季度的用电量如下：
季度名称 | 用电量（单位：千瓦时） |
第一季度 | 250 |
第二季度 | 150 |
第三季度 | 400 |
第四季度 | 200 |
其中各种电器用电量如下表：
各种电器 | 用电量（单位：千瓦时） |
空调 | 250 |
冰箱 | 400 |
照明 | 100 |
彩电 | 150 |
其他 | 100 |
小明根据上面的数据制成下面的统计图.
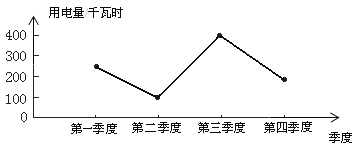
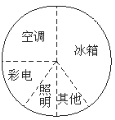
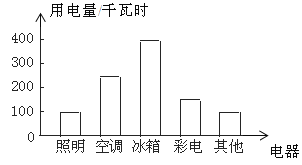
根据以上三幅统计图回答：
（1）从哪幅统计图中可以看出各个季度用电量变化情况？
（2）从哪幅统计图中可以看出冰箱用电量超过总用电量的
？
（3）从哪幅统计图中可以清楚地看出空调的用电量？
