ЬтФПФкШн
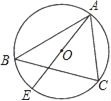
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌЕуEЪЧЯпЖЮBCЕФжаЕуЃЌЗжБ№вдBЃЌCЮЊжБНЧЖЅЕуЕФЁїEABКЭЁїEDCОљЪЧЕШбќжБНЧШ§НЧаЮЃЌЧвдкBCЕФЭЌВрЃЎ
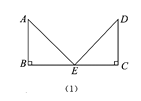
ЃЈ1ЃЉAEКЭEDЕФЪ§СПЙиЯЕЮЊ________ЃЌAEКЭEDЕФЮЛжУЙиЯЕЮЊ________ЃЛ
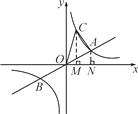
ЃЈ2ЃЉдкЭМЃЈ2ЃЉжаЃЌвдЕуEЮЊЮЛЫЦжааФЃЌзїЁїEGFгыЁїEABЮЛЫЦЃЌЕуHЪЧBCЫљдкжБЯпЩЯЕФвЛЕуЃЌСЌНгGHЃЌHDЃЌЗжБ№ЕУЕНСЫЭМЃЈ2ЃЉКЭЭМЃЈ3ЃЉЃЎ
ЂйдкЭМЃЈ2ЃЉжаЃЌЕуFдкBEЩЯЃЌЁїEGFгыЁїEABЕФЯрЫЦБШЪЧ1ЁУ2ЃЌHЪЧECЕФжаЕуЃЎ
ЧѓжЄЃКGH=HDЃЌGHЁЭHDЃЎ

ЂкдкЭМЃЈ3ЃЉжаЃЌЕуFдкBEЕФбгГЄЯпЩЯЃЌЁїEGFгыЁїEABЕФЯрЫЦБШЪЧkЁУ1ЃЌШєBC=2ЃЌЧыжБНгаДГіCHЕФГЄЮЊЖрЩйЪБЃЌЧЁКУЪЙЕУGH=HDЧвGHЁЭHDЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉAE=EDЃЌAEЁЭEDЃЛЃЈ2ЃЉЂйжЄУїМћНтЮіЃЛЂкCHЕФГЄЮЊkЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЕШбќжБНЧШ§НЧаЮЕФаджЪЕУГіЁїABEЁеЁїDCEЃЌНјЖјЕУГіAE=EDЃЌAEЁЭEDЃЛ
ЃЈ2ЃЉЂйИљОнЁїEGFгыЁїEABЕФЯрЫЦБШ1ЃК2ЃЌЕУГіEH=HC=![]() ECЃЌНјЖјЕУГіЁїHGFЁеЁїDHCЃЌМДПЩЧѓГіGH=HDЃЌGHЁЭHDЃЛ
ECЃЌНјЖјЕУГіЁїHGFЁеЁїDHCЃЌМДПЩЧѓГіGH=HDЃЌGHЁЭHDЃЛ
ЂкИљОнЧЁКУЪЙGH=HDЧвGHЁЭHDЪБЃЌЕУГіЁїGFHЁеЁїHCDЃЌНјЖјЕУГіCHЕФГЄЃЎ
ЃЈ1ЃЉЁпЕуEЪЧЯпЖЮBCЕФжаЕуЃЌЗжБ№BCвдЮЊжБНЧЖЅЕуЕФЁїEABКЭЁїEDCОљЪЧЕШбќШ§НЧаЮЃЌ
ЁрBE=EC=DC=ABЃЌЁЯB=ЁЯC=90ЁуЃЌ
ЁрЁїABEЁеЁїDCEЃЌ
ЁрAE=DEЃЌ
ЁЯAEB=ЁЯDEC=45ЁуЃЌ
ЁрЁЯAED=90ЁуЃЌ
ЁрAEЁЭEDЃЎ
ЙЪД№АИЮЊЃКAE=EDЃЌAEЁЭEDЃЛ
ЃЈ2ЃЉЂйгЩЬтвтЃЌЁЯB=ЁЯC=90ЁуЃЌAB=BE=EC=DCЃЌ
ЁпЁїEGFгыЁїEABЕФЯрЫЦБШ1ЃК2ЃЌ
ЁрЁЯGFE=ЁЯB=90ЁуЃЌGF=![]() ABЃЌEF=
ABЃЌEF=![]() EBЃЌ
EBЃЌ
ЁрЁЯGFE=ЁЯCЃЌ
ЁрEH=HC=![]() ECЃЌ
ECЃЌ
ЁрGF=HCЃЌFH=FE+EH=![]() EB+
EB+![]() EC=
EC=![]() BC=EC=CDЃЌ
BC=EC=CDЃЌ
ЁрЁїHGFЁеЁїDHCЃЎ
ЁрGH=HDЃЌЁЯGHF=ЁЯHDCЃЎ
ЁпЁЯHDC+ЁЯDHC=90ЁуЃЎ
ЁрЁЯGHF+ЁЯDHC=90Ёу
ЁрЁЯGHD=90ЁуЃЎ
ЁрGHЁЭHDЃЎ
ЂкИљОнЬтвтЕУГіЃКЁпЕБGH=HDЃЌGHЁЭHDЪБЃЌ
ЁрЁЯFHG+ЁЯDHC=90ЁуЃЌ
ЁпЁЯFHG+ЁЯFGH=90ЁуЃЌ
ЁрЁЯFGH=ЁЯDHCЃЌ
Ёр ЃЌ
ЃЌ
ЁрЁїGFHЁеЁїHCDЃЌ
ЁрCH=FGЃЌ
ЁпEF=FGЃЌ
ЁрEF=CHЃЌ
ЁпЁїEGFгыЁїEABЕФЯрЫЦБШЪЧkЃК1ЃЌBC=2ЃЌ
ЁрBE=EC=1ЃЌ
ЁрEF=kЃЌ
ЁрCHЕФГЄЮЊkЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ