题目内容
【题目】请在下列横线上注明理由.
如图,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在边
在边![]() 上,点
上,点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,点
,点![]() 到
到![]() 和
和![]() 的距离相等.求证:点
的距离相等.求证:点![]() 到
到![]() 和
和![]() 的距离相等.
的距离相等.
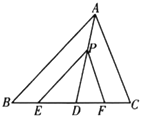
证明:∵![]() (已知),
(已知),
∴![]() (______),
(______),
∴![]() (______),
(______),
∵![]() (已知),
(已知),
∴![]() (______),
(______),
∵点![]() 到
到![]() 和
和![]() 的距离相等(已知),
的距离相等(已知),
∴![]() 是
是![]() 的角平分线(______),
的角平分线(______),
∴![]() (角平分线的定义),
(角平分线的定义),
∴![]() (______),
(______),
即![]() 平分
平分![]() (角平分线的定义),
(角平分线的定义),
∴点![]() 到
到![]() 和
和![]() 的距离相等(______).
的距离相等(______).
【答案】同位角相等,两直线平行;两直线平行,同位角相等;两直线平行,同位角相等;角的内部到角的两边距离相等的点在角的平分线上;等量代换;角平分线上的点到角的两边的距离相等.
【解析】
根据角平分线的性质及平行线的性质与判定即可解答.
证明:∵∠PFD=∠C(已知),
∴PF∥AC(同位角相等,两直线平行),
∴∠DPF=∠DAC(两直线平行,同位角相等).
∵PE∥AB(已知),
∴ ∠EPD=∠BAD(两直线平行,同位角相等).
∵点 D到PE和PF的距离相等(已知),
∴ PD是 ∠EPF的角平分线(角的内部到角的两边距离相等的点在角的平分线上),
∴ ∠EPD=∠FPD(角平分线的定义),
∴∠BAD=∠DAC (等量代换),
即AD平分∠BAC (角平分线的定义),
∴点D到AB和AC的距离相等(角平分线上的点到角的两边的距离相等)

练习册系列答案
相关题目