题目内容
(2012•绵阳)如图1,在直角坐标系中,O是坐标原点,点A在y轴正半轴上,二次函数y=ax2+
x+c的图象F交x轴于B、C两点,交y轴于M点,其中B(-3,0),M(0,-1).已知AM=BC.
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N.
①若直线l⊥BD,如图1,试求
+
的值;
②若l为满足条件的任意直线.如图2.①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例.

| 1 |
| 6 |
(1)求二次函数的解析式;
(2)证明:在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形,并请求出直线BD的解析式;
(3)在(2)的条件下,设直线l过D且分别交直线BA、BC于不同的P、Q两点,AC、BD相交于N.
①若直线l⊥BD,如图1,试求
| 1 |
| BP |
| 1 |
| BQ |
②若l为满足条件的任意直线.如图2.①中的结论还成立吗?若成立,证明你的猜想;若不成立,请举出反例.

分析:(1)利用待定系数法求出二次函数的解析式;
(2)首先求出D点的坐标,可得AD=BC且AD∥BC,所以四边形ABCD是平行四边形;再根据B、D点的坐标,利用待定系数法求出直线BD的解析式;
(3)本问的关键是判定平行四边形ABCD是菱形.
①推出AC∥直线l,从而根据平行线间的比例线段关系,求出BP、CQ的长度,计算出
+
=
;
②判定△PAD∽△DCQ,得到AP•CQ=25,利用这个关系式对
+
进行分式的化简求值,结论为
+
=
不变.
(2)首先求出D点的坐标,可得AD=BC且AD∥BC,所以四边形ABCD是平行四边形;再根据B、D点的坐标,利用待定系数法求出直线BD的解析式;
(3)本问的关键是判定平行四边形ABCD是菱形.
①推出AC∥直线l,从而根据平行线间的比例线段关系,求出BP、CQ的长度,计算出
| 1 |
| BP |
| 1 |
| BQ |
| 1 |
| 5 |
②判定△PAD∽△DCQ,得到AP•CQ=25,利用这个关系式对
| 1 |
| BP |
| 1 |
| BQ |
| 1 |
| BP |
| 1 |
| BQ |
| 1 |
| 5 |
解答:解:(1)∵二次函数y=ax2+
x+c的图象经过点B(-3,0),M(0,-1),
∴
,
解得a=
,c=-1.
∴二次函数的解析式为:y=
x2+
x-1.
(2)由二次函数的解析式为:y=
x2+
x-1,
令y=0,得
x2+
x-1=0,
解得x1=-3,x2=2,∴C(2,0),∴BC=5;
令x=0,得y=-1,∴M(0,-1),OM=1.
又AM=BC,∴OA=AM-OM=4,∴A(0,4).
设AD∥x轴,交抛物线于点D,如图1所示,
则yD=
x2+
x-1=OA=4,
解得x1=5,x2=-6(位于第二象限,舍去)
∴D点坐标为(5,4).
∴AD=BC=5,
又∵AD∥BC,
∴四边形ABCD为平行四边形.
即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形.
设直线BD解析式为:y=kx+b,∵B(-3,0),D(5,4),
∴
,
解得:k=
,b=
,
∴直线BD解析式为:y=
x+
.
(3)在Rt△AOB中,AB=
=5,又AD=BC=5,∴?ABCD是菱形.
①若直线l⊥BD,如图1所示.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴AC∥直线l,
∴
=
=
=
,
∵BA=BC=5,
∴BP=BQ=10,
∴
+
=
+
=
;
②若l为满足条件的任意直线,如图2所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,
∴△PAD∽△DCQ,
∴
=
,
∴AP•CQ=AD•CD=5×5=25.
∴
+
=
+
=
+
=
=
=
=
.
| 1 |
| 6 |
∴
|
解得a=
| 1 |
| 6 |
∴二次函数的解析式为:y=
| 1 |
| 6 |
| 1 |
| 6 |
(2)由二次函数的解析式为:y=
| 1 |
| 6 |
| 1 |
| 6 |
令y=0,得
| 1 |
| 6 |
| 1 |
| 6 |
解得x1=-3,x2=2,∴C(2,0),∴BC=5;
令x=0,得y=-1,∴M(0,-1),OM=1.
又AM=BC,∴OA=AM-OM=4,∴A(0,4).
设AD∥x轴,交抛物线于点D,如图1所示,
则yD=
| 1 |
| 6 |
| 1 |
| 6 |
解得x1=5,x2=-6(位于第二象限,舍去)
∴D点坐标为(5,4).
∴AD=BC=5,
又∵AD∥BC,
∴四边形ABCD为平行四边形.
即在抛物线F上存在点D,使A、B、C、D四点连接而成的四边形恰好是平行四边形.
设直线BD解析式为:y=kx+b,∵B(-3,0),D(5,4),
∴
|
解得:k=
| 1 |
| 2 |
| 3 |
| 2 |
∴直线BD解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)在Rt△AOB中,AB=
| OA2+OB2 |
①若直线l⊥BD,如图1所示.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴AC∥直线l,
∴
| BA |
| BP |
| BC |
| BQ |
| BN |
| BD |
| 1 |
| 2 |
∵BA=BC=5,
∴BP=BQ=10,
∴
| 1 |
| BP |
| 1 |
| BQ |
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 5 |
②若l为满足条件的任意直线,如图2所示,此时①中的结论依然成立,理由如下:
∵AD∥BC,CD∥AB,
∴△PAD∽△DCQ,
∴
| AP |
| CD |
| AD |
| CQ |
∴AP•CQ=AD•CD=5×5=25.
∴
| 1 |
| BP |
| 1 |
| BQ |
=
| 1 |
| AB+AP |
| 1 |
| BC+CQ |
=
| 1 |
| 5+AP |
| 1 |
| 5+CQ |
=
| (5+AP)+(5+CQ) |
| (5+AP)(5+CQ) |
=
| 10+AP+CQ |
| 25+5(AP+CQ)+AP•CQ |
=
| 10+AP+CQ |
| 50+5(AP+CQ) |
=
| 1 |
| 5 |
点评:本题考查了二次函数压轴题,正确解答本题需要熟练掌握函数的图象与性质(二次函数与一次函数)、平面图形的性质与应用(平行四边形、菱形、相似三角形、平行线等).本题涉及考点较多,虽有一点的难度,但相信不少考生均可顺利解答.第(3)问中,需要注意平行四边形ABCD是菱形,这样后续的计算均可迎刃而解.

练习册系列答案
相关题目
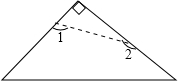 (2012•绵阳)如图,将等腰直角三角形虚线剪去顶角后,∠1+∠2=( )
(2012•绵阳)如图,将等腰直角三角形虚线剪去顶角后,∠1+∠2=( ) (2012•绵阳)如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )
(2012•绵阳)如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( )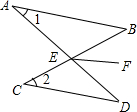 (2012•绵阳)如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=
(2012•绵阳)如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=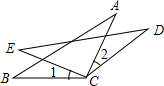 (2012•绵阳)如图,BC=EC,∠1=∠2,要使△ABC≌△DEC,则应添加的一个条件为
(2012•绵阳)如图,BC=EC,∠1=∠2,要使△ABC≌△DEC,则应添加的一个条件为 (2012•绵阳)如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积为
(2012•绵阳)如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积为