题目内容
 如图,在半径为
如图,在半径为| 5 |
 |
| AB |
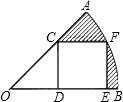
分析:首先要明确S阴影=S扇形OAB-S△OCD-S正方形CDEF,然后依面积公式计算即可.
解答:解:连接OF,

∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
于是在Rt△OFE中,OE=2EF,
∵OF=
,EF2+OE2=OF2,
∴EF2+(2EF)2=5,
解得:EF=1,
∴EF=OD=CD=1,
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=
-
×1×1-1×1=
π-
.
故选A.

∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
于是在Rt△OFE中,OE=2EF,
∵OF=
| 5 |
∴EF2+(2EF)2=5,
解得:EF=1,
∴EF=OD=CD=1,
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=
45π×(
| ||
| 360 |
| 1 |
| 2 |
| 5 |
| 8 |
| 3 |
| 2 |
故选A.
点评:本题失分率较高,学生的主要失误在于找不到解题的切入点,不知道如何添加辅助线,也有学生对直角三角形三边关系不熟悉,误认为∠FOB=30°造成失误.

练习册系列答案
相关题目
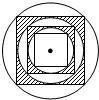 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
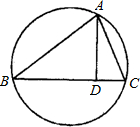 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD=
8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD= 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是