题目内容
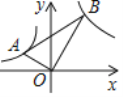
【题目】在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,若sin∠BAO =
(x>0)的图象上,若sin∠BAO = ![]() ,则k的值为__________.
,则k的值为__________.
【答案】-1
【解析】
过点A、B分别作AD⊥x轴,BE⊥x轴,垂足为D、E,证明△AOD∽△OBE,得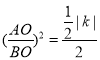 ,由sin∠BAO =
,由sin∠BAO = ![]() 得
得![]() ,求出满足条件的k的值即可.
,求出满足条件的k的值即可.
过点A、B分别作AD⊥x轴,BE⊥x轴,垂足为D、E,

∵∠AOB=90°
∴∠AOD+∠∠BOE=90°,
∵∠OBE+∠BOE=90°
∴∠AOD=∠OBE,
∵∠ADO=∠BEO=90°
∴△AOD∽△OBE,
∴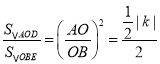 ,
,
∵sin∠BAO =![]() ,
,
设BO=![]() ,则AB=5x,AO=
,则AB=5x,AO=![]()
∴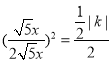 ,整理得,|k|=1
,整理得,|k|=1
∴k=±1,
∵k<0,
∴k=-1.
故答案为:-1.

练习册系列答案
相关题目
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
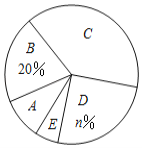
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.