题目内容
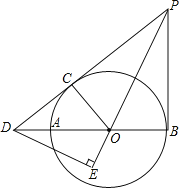
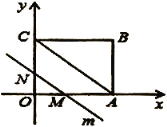
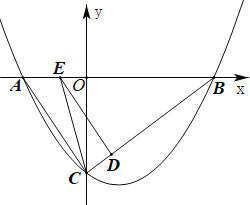
【题目】已知抛物线![]() 交x轴于A(-2,0),B(4,0)两点,交y轴于C点,连接AC、BC.点D在线段BC上(不与点B、点C重合),DE∥AC,交x轴于点E,连接CE.
交x轴于A(-2,0),B(4,0)两点,交y轴于C点,连接AC、BC.点D在线段BC上(不与点B、点C重合),DE∥AC,交x轴于点E,连接CE.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△CDE的面积为S.则m为何值时,S取得最大值,并求出这个最大值;
(3)若△ACE为等腰三角形,请直接写出此时点D的坐标.
【答案】(1)![]() ;(2)m=2时,S取得最大值
;(2)m=2时,S取得最大值![]() ;(3)
;(3)![]() 或
或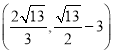 或
或![]()
【解析】
(1)根据待定系数法解答即可;
(2)易得点C坐标和BC的长,然后利用待定系数法即可求出直线BC的解析式,如图1,作DF⊥x轴于点F,则DF的长可用含m的代数式表示,由DE∥AC可得△BDE∽△BCA,于是有![]() ,由DF∥OC可得
,由DF∥OC可得![]() ,于是有,
,于是有,![]() 则BE可用含m的代数式表示,然后根据
则BE可用含m的代数式表示,然后根据![]() 即可得出S与m的函数关系式,再利用二次函数的性质即可求出结果;
即可得出S与m的函数关系式,再利用二次函数的性质即可求出结果;
(3)分三种情况:当CA=CE时,如图2,结合(2)题中的BE先用含m的代数式表示AE,由AE=2AO即可建立m的方程,解方程即可求出m,进而可得点D坐标;当AC=AE时,如图3,由AC的长可直接解出m,从而可得点D坐标;当EA=EC时,如图4,在Rt△OEC中,根据勾股定理建立m的方程,解方程即可求出m,于是可得点D坐标.
解:(1)∵抛物线![]() 交x轴于A(﹣2,0),B(4,0)两点,
交x轴于A(﹣2,0),B(4,0)两点,
∴![]() ,解得:
,解得: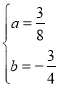 ,
,
∴抛物线解析式为![]() ;
;
(2)抛物线![]() 与y轴交于点C(0,﹣3),
与y轴交于点C(0,﹣3),
∵A(﹣2,0),B(4,0),
∴OA=2,OC=3,OB=4.
在Rt△OBC中,BC=![]() .
.
由B(4,0)、C(0,﹣3)可求得直线BC的解析式为![]() ,
,
∵点D的横坐标为m,∴D(m,![]() ),
),
如图1,作DF⊥x轴于点F,
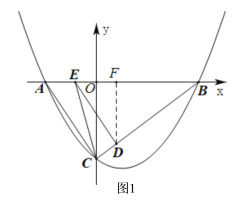
∴DF=![]() ,
,
∵DE∥AC,
∴△BDE∽△BCA.
∴![]() .
.
∵DF∥OC,
∴![]() .
.
∴![]() .
.
∴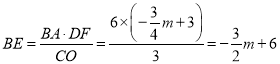 .
.
∴![]() ,
,
∴m=2时,S取得最大值![]() ;
;
(3)分三种情况:
当CA=CE时,如图2,
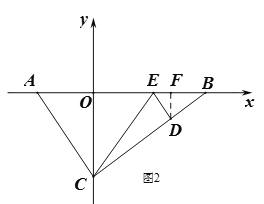
∵![]() ,
,
∴AE=![]() ,
,
∵AE=2AO=4,
∴![]() ,解得:
,解得:![]() ,
,
此时点D的坐标是:![]() ;
;
当AC=AE时,如图3,
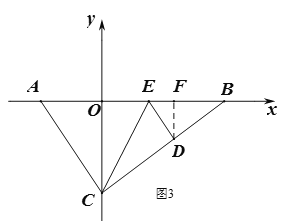
∵![]() ,
,
∴![]()
∴![]() ,
,
此时点M的坐标为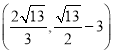 ;
;
当EA=EC时,如图4,
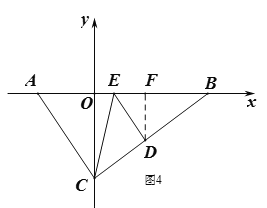
∵![]() ,∴
,∴![]()
则在Rt△OEC中,由勾股定理,得:![]() ,解得:
,解得:![]() ,
,
此时点D的坐标是![]() .
.
综上,点D的坐标为![]() 或
或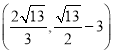 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买![]() 商品共花去了
商品共花去了![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?