题目内容
【题目】如图,已知双曲线y= ![]() ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC. 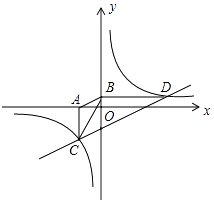
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式y1;
(3)根据图象直接写出y≥y1时,x的取值范围.
【答案】
(1)解:∵y= ![]() ,经过点D(6,1),
,经过点D(6,1),
∴ ![]() =1,
=1,
∴k=6;
(2)解:∵点D(6,1),
∴BD=6,
设△BCD边BD上的高为h,
∵△BCD的面积为12,
∴ ![]() BDh=12,即
BDh=12,即 ![]() ×6h=12,解得h=4,
×6h=12,解得h=4,
∴CA=3,
∴ ![]() =﹣3,解得x=﹣2,
=﹣3,解得x=﹣2,
∴点C(﹣2,﹣3),
设直线CD的解析式为y=kx+b,
则 ![]() ,
,
得  ,
,
所以,直线CD的解析式为y= ![]() x﹣2,
x﹣2,
(3)解:∵点D(6,1),点C(﹣2,﹣3),
∴当y≥y1时,x的取值范围为:x≤﹣2,0<x≤6.
【解析】(1)把点D的坐标代入双曲线解析式,进行计算即可得解;(2)先根据点D的坐标求出BD的长度,再根据三角形的面积公式求出点C到BD的距离,然后求出点C的纵坐标,再代入反比例函数解析式求出点C的坐标,然后利用待定系数法求一次函数解析式解答;(3)根据函数图象即可得到结论.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目