Question

已知点A（-1，n）（n＞0）和点B（2，3）在抛物线y₁=x²+bx+c上，点C（1，0）是x轴上一点，且CA+CB的值最小．
（1）求抛物线y₁的解析式．
（2）左右平移抛物线y₁=ax²+bx+c，记平移后点A的对应点为A′，点B的对应点为B′，点E（-1，0）和点F（-3，0）是x轴上两个定点，问是否存在某个位置，使四边形A′B′EF的周长最短？若存在，求出此时抛物线的解析式；若不存在，请说明理由．
（3）平移抛物线y₁=ax²+bx+c得到y₂=（x-h）²，当2＜x≤m时，有y₂≤x恒成立，当m取最大值时，求h的值．

Answer 1

分析：（1）此题的关键是确定出点A的坐标，那么必须从CA+CB的值最小入手；解题思路和该类型题是一样的，首先作点B关于x轴的对称点，然后求出过该对称点C的直线，那么当CA+CB值最小时，点A、C以及点B关于x轴的对称点必共线，所以将点A坐标代入上面所得的直线解析式中即可确定点A的坐标，再利用待定系数法来确定抛物线的解析式；
（2）抛物线平移时，点A′、B′平移的程度是相同的，那么先判断一下平移的大致方向，然后用平移的距离表示出点A′、B′的坐标，显然在四边形A′B′EF中，线段A′B′与线段EF的长是一定的，当这个四边形的周长最小时，A′F+B′E的值最小，但这涉及到四个点，无法应用（1）的解题思路，所以要对图形做适当处理；观察图形可知，EF=2，那么将点B′向左平移2个单位，得到点B″，显然四边形B″B′EF是个平行四边形，有B″F=B′E，所以将问题转化为A′F+B″F的值最小，这样转化为类似（1）的问题，按（1）的思路来解即可；
（3）这个小题要结合函数的图象来解，关键的问题在于对“y₂≤x”，如果将上式看作简单的不等式，这道题将很难解出，所以可以将x看作一次函数，确定了这个思路后再进一步进行分析，首先设 y₃=x（这是一个一次函数），那么y₂＜x可改为y₂＜y₃，在函数图象上，可以理解为：在“2＜x≤m”区间内，直线y₃的函数图象在抛物线y₂的函数图象上方，然后通过作图不难判断出m的最大值以及函数y₂经过的定点，据此确定h的值．

解答：解：（1）取点B关于x轴的对称点（2，-3）；
设直线AC的解析式为：y=kx+b，若CA+CB的值最小，那么点（2，-3）必在直线AC上，有：

2k+b=-3 k+b=0

，
解得

k=-3 b=3

故直线AC：y=-3x+3，则点A（-1，6）；
已知抛物线y₁=x²+bx+c过点A、B，依题意，有：

1-b+c=6 4+2b+c=3

，
解得

b=-2 c=3

．
故抛物线y₁=x²-2x+3；

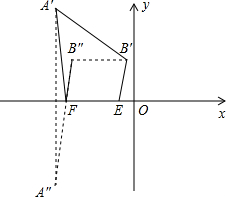（2）①若抛物线向右平移，则有AF+BE＞A′F+B′E，所以不能向右平移．
②当抛物线向左平移时，设平移后点A对应的点A′为（-1-t，6），点B对应的点B′为（2-t，3）；（如右图）
将点B?向左平移2个单位得点B″（-t，3），此时四边形B″B′EF是平行四边形，则 B′E=B″F；
四边形A′B′EF中，A′B′、EF是定值，若四边形A′B′EF的周长最短，那么 A′F+B′E（即A′F+B′F）最小．
同（1）的思路，取点A′关于x轴对称的点A″为（-1-t，-6），则直线A″B″解析式为：y=9x+9t+3；
将点F（-3，0）代入直线A″B″的解析式中，得t=

8

3

；
则此时四边形A′B′EF的周长最小．
所以平移后的抛物线解析式为：y=(x-1+

8

3

)2+2，
即y=(x+

5

3

)2+2；

（3）令y₃=x，则y₂≤y₃；
如右图，当抛物线y₂左分支过点（2，2）时，抛物线y₂与直线y₃的另一交点横坐标则为m的最大值；
将点（2，2）代入y₂=（x-h）²，得：
（2-h）²=2，
解得：h₁=2+

2

，h₂=2-

2

（舍）；
则h=2+

2

．

点评：考查了二次函数综合题，该题主要涉及了：函数解析式的确定、轴对称图形的性质以及两点间线段最短的综合应用、利用函数图象解不等式等重要知识；着重体现了数形结合思想的实际应用．