题目内容
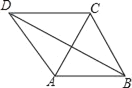
【题目】已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
【答案】cos∠DBA=![]() .
.
【解析】
欲求∠DBA的余弦值,需将已知条件构建到一个直角三角形中求解;已知四边形ABCD中,AB=AC=AD;若以A为圆心,AB为半径作圆,则此圆必过C、D;延长BA交⊙A于E,则BE为⊙A的直径,连接DE.在Rt△BDE中,已知了BE=2a,需求出BD的长;根据DC∥AB,易证得DE=BC=b,则根据勾股定理即可求得BD的长,由此得解.
如图,以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED.
∵AB∥CD,∴∠CAB=∠DCA,∠DAE=∠CDA.
∵AC=AD,∴∠DCA=∠CDA,∴∠DAE=∠CAB.
在△ABC和△DAE中,∵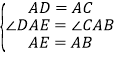 ,∴△CAB≌△DAE(SAS),∴ED=BC=b.
,∴△CAB≌△DAE(SAS),∴ED=BC=b.
∵BE是直径,∴∠EDB=90°.
在Rt△EDB中,ED=b,BE=2a,由勾股定理得:ED2+BD2=BE2,∴BD![]() ,∴cos∠DBA
,∴cos∠DBA![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目