题目内容
【题目】如图，已知直线l：y＝﹣
x+8交x轴于点E，点A为x轴上的一个动点（点A不与点E重合），在直线l上取一点B（点B在x轴上方），使BE＝5AE，连接AB，以AB为边沿顺时针方向作正方形ABCD，连结OB，以OB为直径作⊙P．
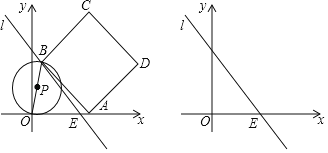
（1）当点A在点E右侧时．
①若点B刚好落在y轴上，则线段BE的长为 ，点D的坐标为 ．
②若点A的坐标为（9，0），求正方形ABCD的边长．
（2）⊙P与正方形ABCD的边相切于点B，求点B的坐标．
（3）点Q为⊙P与直线BE的交点，连接CQ，当CQ平分∠BCD时，点B的坐标为 ．（直接写出答案）
【答案】（1）①BE＝10，D（16，8）；②12
；（2）点B的坐标为（﹣12，24）或（
，）；（3）B（﹣
，
）．
【解析】
（1）①利用勾股定理求出BE即可，证明
和
都是等腰直角三角形即可解决问题；
②如图2中，作BH⊥x轴于H，求出点B的坐标，利用勾股定理即可解决问题；
（2）如图3中，当点A与原点O重合时，⊙P与BC相切于点B，AE＝6，即可求出.
如图4中，当OB⊥AB时，⊙P与AB相切于点B，作BH⊥OA于H．设AE＝m，则BE＝5m，BH＝4m，EH＝3m，证明
是等腰直角三角形，即可解决问题；
（3）如图5中，如图作BH⊥x轴于H．连接OQ．设AE＝k，则BE＝5k，BH＝4k，EH＝3k，求得直线OQ的解析式，再求得直线l与直线OQ的交点Q的坐标，利用平行分线段成比例，即可解决问题.
解：（1）①如图1中，作DG⊥x轴于G．
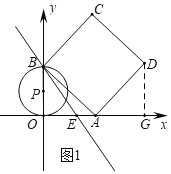
由题意：E（6，0），B（0，8），
∴OE＝6，OB＝8，
∴BE＝
＝10，
∵BE＝5AE，
∴AE＝2，
∴OA＝8，
∴OB＝OA＝8，
∵AB＝AD＝8，∠BAD＝90°，
∴∠BAO＝∠DAG＝45°，
∵DG⊥AG，
∴DG＝AG＝8，
∴OG＝16，
∴D（16，8），
②如图2中，作BH⊥x轴于H．
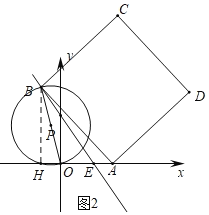
∵A（9，0），
∴OA＝9，
∵OE＝6，
∴AE＝3，
∵BE＝5AE，
∴BE＝15，
∵BH：EH＝4：3，
∴BH＝12，EH＝9，
∴AH＝12，
∴AB＝
＝12 ．
（2）如图3中，当点A与原点O重合时，⊙P与BC相切于点B，AE＝6，
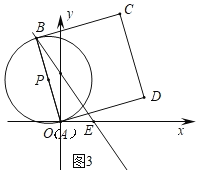
∵BE＝5AE，
∴BE＝30，可得B（﹣12，24）．
如图4中，当OB⊥AB时，⊙P与AB相切于点B，作BH⊥OA于H．
设AE＝m，则BE＝5m，BH＝4m，EH＝3m，
∴BH＝AH＝4m，
∴∠BAO＝45°，
∵∠OBA＝90°，
∴∠BOA＝45°，
∴点B的横坐标与纵坐标相同，可得B（，），
综上所述，满足条件的点B的坐标为（﹣12，24）或（，）．
（3）如图5中，如图作BH⊥x轴于H．连接OQ．设AE＝k，则BE＝5k，BH＝4k，EH＝3k，
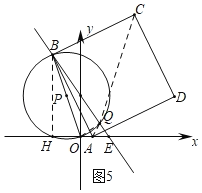
∴AH＝2k，
可得B（6﹣3k，4k），C（k+6，6k），A（6﹣k，0），
∵OQ⊥BE，
∴直线OQ的解析式为：y＝
x，
由
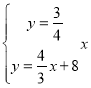，解得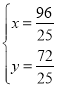
，
∴Q（
，
），
∴CQ平分∠BCD，
∴A，C，Q共线，
∴
，
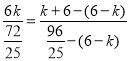解得k＝
，
∴B（
，）．
