Question

【题目】如图，已知画射线，射线，试写出和的数量关系，并说明理由.

Answer 1

【答案】或，见解析.

【解析】

分OC、OD在边OA的同侧和异侧分别作出图形，然后分别进行计算即可得解．

∠AOB=∠COD或∠AOB+∠COD=180°，理由如下：

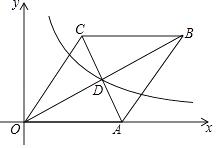
如图1，∵OC⊥OA，OD⊥OB，

∴∠AOB+∠BOC=90°，∠COD+∠BOC=90°，

∴∠AOB=∠COD；

如图2，∵OC⊥OA，OD⊥OB，

∴∠AOC=∠BOD=90°，

∴∠AOB+∠BOC=∠AOB+∠AOD=90°，

∴∠AOB+∠BOC+∠AOB+∠AOD=180°，

又∵∠BOC+∠AOB+∠AOC=∠COD，

∴∠AOB+∠COD=180°；

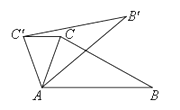
如图3，∠AOB+∠COD =360°-∠AOC-∠BOD=360°-90°-90°=180°；

如图4，∵OC⊥OA，OD⊥OB，

∴∠AOB+∠AOD=90°，∠COD+∠AOD=90°，

∴∠AOB=∠COD；

综上所述，∠AOB=∠COD或∠AOB+∠COD=180°.