题目内容
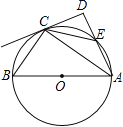
【题目】如图,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() 是
是![]() 的直径,
的直径,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
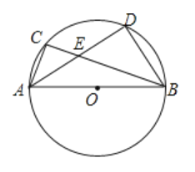
![]() 求证:
求证:![]() ;
;
![]() ①当四边形
①当四边形![]() 为平行四边形时,
为平行四边形时,![]() 的长为 ;
的长为 ;
②若![]() ,则
,则![]() 的长为 (结果保留
的长为 (结果保留![]() )
)
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)先根据角平分线的定义可得![]() ,再根据圆周角定理可得
,再根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,然后根据相似三角形的判定即可得证;
,然后根据相似三角形的判定即可得证;
(2)①先根据菱形的判定与性质可得![]() ,再根据等边三角形的判定与性质可得
,再根据等边三角形的判定与性质可得![]() ,然后根据圆周角定理、直角三角形的性质可得
,然后根据圆周角定理、直角三角形的性质可得![]() ,最后根据(1)相似三角形的性质可得
,最后根据(1)相似三角形的性质可得![]() ,从而可得DE的长,由此即可得出答案;
,从而可得DE的长,由此即可得出答案;
②先根据三角形的外角性质可得![]() ,再根据三角形的内角和定理可得
,再根据三角形的内角和定理可得![]() ,从而可得
,从而可得![]() ,然后根据等腰三角形的性质、三角形的内角和定理可得
,然后根据等腰三角形的性质、三角形的内角和定理可得![]() ,最后利用弧长公式计算即可得.
,最后利用弧长公式计算即可得.
(1)![]() 平分
平分![]()
![]()
由圆周角定理得:![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,![]()
![]() ;
;
(2)①如图,连接OC、OD、CD
![]() 四边形
四边形![]() 为平行四边形,且
为平行四边形,且![]()
![]() 平行四边形
平行四边形![]() 是菱形
是菱形
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
由圆周角定理得:![]()
在![]() 中,
中,![]() ,
,![]()
![]()
由(1)知,![]()
![]() ,即
,即![]()
解得![]()
则![]()
故答案为:![]() ;
;
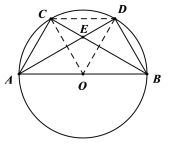
②如图,连接OD
![]()
![]()
由(1)已得:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
则![]() 的长为
的长为![]()
故答案为:![]() .
.


练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目