题目内容
【题目】定义:函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,点
轴对称,点![]() 是
是![]() 轴上一点,将函数
轴上一点,将函数![]() 的图象位于直线
的图象位于直线![]() 左侧的部分,以
左侧的部分,以![]() 轴为对称轴翻折,得到新的函数
轴为对称轴翻折,得到新的函数![]() 的图象,我们称函数
的图象,我们称函数![]() 是函数
是函数![]() 的对称折函数,函数
的对称折函数,函数![]() 的图象记作
的图象记作![]() ,函数
,函数![]() 的图象位于直线
的图象位于直线![]() 上以及右侧的部分记作
上以及右侧的部分记作![]() ,图象
,图象![]() 和
和![]() 合起来记作图象
合起来记作图象![]() .
.
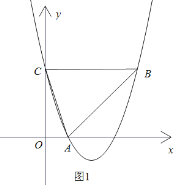
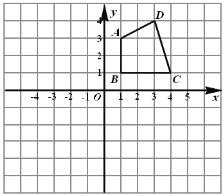
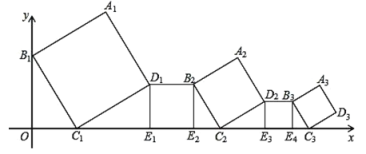
例如:如图,函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为
的解析式为![]() .
.
(1)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的对称折函数
时,它的对称折函数![]() 的解析式为_______;
的解析式为_______;
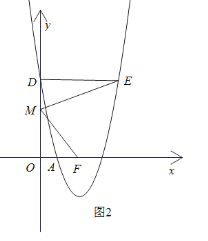
(2)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 且
且![]() 时,求图象
时,求图象![]() 上点的纵坐标的最大值和最小值;
上点的纵坐标的最大值和最小值;
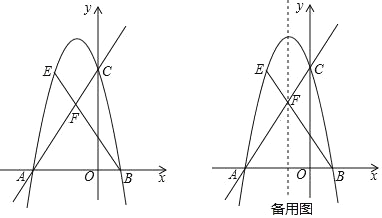
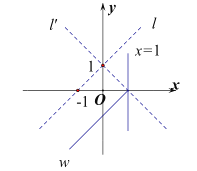
(3)函数![]() 的解析式为
的解析式为![]() .若
.若![]() ,直线
,直线![]() 与图象
与图象![]() 有两个公共点,求
有两个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的解析式为
的解析式为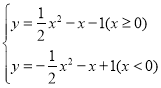 ;图象
;图象![]() 上的点的纵坐标的最大值为
上的点的纵坐标的最大值为![]() ,最小值为
,最小值为![]() ;(3)当
;(3)当![]() ,
,![]() ,
,![]() 时,直线
时,直线![]() 与图象
与图象![]() 有两个公共点.
有两个公共点.
【解析】
(1)根据对折函数的定义直接写出函数解析式即可;
(2)先根据题意确定F的解析式,然后根据二次函数的性质确定函数的最大值和最小值即可;
(3)先求出当a=1时图像F的解析式,然后分![]() 、点
、点![]() 落在
落在![]() 上和点
上和点![]() 落在
落在![]() 上三种情况解答,最后根据图像即可解答.
上三种情况解答,最后根据图像即可解答.
解:(1)![]()
(2)![]() 的解析式为
的解析式为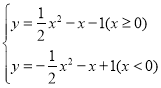
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴图象![]() 上的点的纵坐标的最大值为
上的点的纵坐标的最大值为![]() ,最小值为
,最小值为![]() .
.
(3)当![]() 时,图象
时,图象![]() 的解析式为
的解析式为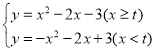
∴该函数的最大值和最小值分别为4和-4;
a:当![]() 时,
时,![]() ,
,
∴当![]() 时直线
时直线![]() 与图象
与图象![]() 有两个公共点;
有两个公共点;
b:当点![]() 落在
落在![]() 上时,
上时,
![]() ,解得
,解得![]() ,
,![]()
c:当点![]() 落在
落在![]() 上时,
上时,
![]() ,解得
,解得![]() (舍),
(舍),![]()
![]() ,
,
∴![]()
∴当![]() 或
或![]() 时,直线
时,直线![]() 与图象
与图象![]() 有两个公共点;
有两个公共点;
综上所述:当![]() ,
,![]() ,
,![]() 时,直线
时,直线![]() 与图象
与图象![]() 有两个公共点.
有两个公共点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目