题目内容
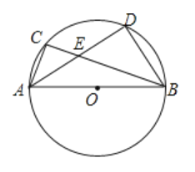
【题目】已知:二次函数y=x2-2mx-m2+4m-2的对称轴为l,抛物线与y轴交于点C,顶点为D.

(1)判断抛物线与x轴的交点情况;
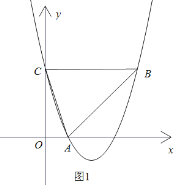
(2)如图1,当m=1时,点P为第一象限内抛物线上一点,且△PCD是以PD为腰的等腰三角形,求点P的坐标;
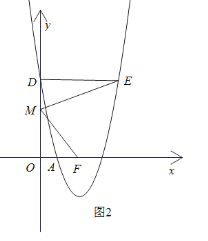
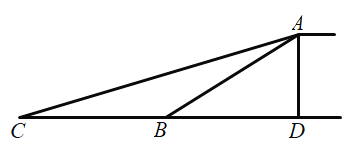
(3)如图2,直线![]() 和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,
和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,![]() 时,求h的最大值.
时,求h的最大值.
【答案】(1)证明见解析;(2)点![]() 的坐标为
的坐标为![]() 或
或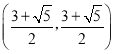 或
或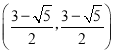 ;(3)
;(3)![]() 最大值为4.
最大值为4.
【解析】
(1)令y=0,转化为一元二次方程,求出△=8(m-1)2,即可得出结论;
(2)先求出点C,D坐标,再分两种情况,判断出点P是CD的中垂线或CP的中垂线,即可得出结论;
(3)利用点M在抛物线对称轴上,和MO=BM表示出点B坐标,代入抛物线解析式中,求出m,进而得出抛物线解析式,再得出![]() ,即可得出结论.
,即可得出结论.
解:(1)针对于二次函数y=x2-2mx-m2+4m-2,
令y=0,则x2-2mx-m2+4m-2=0,
∴![]()
不论![]() 取何值,
取何值,![]()
∴抛物线与![]() 轴至少有一个交点(或一定有交点).
轴至少有一个交点(或一定有交点).
(2)当![]() 时,
时,![]() ∴点
∴点![]() 、点
、点![]()
当![]() 时,可知点
时,可知点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴点![]() 坐标为
坐标为![]()
当![]() 时,点
时,点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
∵![]() ∴点
∴点![]() 在直线
在直线![]() 上
上
∴![]() 解得
解得![]()
∴点![]() 坐标为
坐标为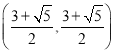 和
和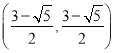 .
.
综上,点![]() 的坐标为
的坐标为![]() 或
或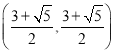 或
或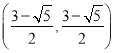 .
.
(3)当![]() 时,
时,
∵![]()
∴点![]() 的横坐标为
的横坐标为![]() ,则纵坐标
,则纵坐标![]()
点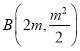 ,
,
把点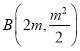 代入抛物线得:
代入抛物线得:![]()
解得![]() ,
,![]() (舍去)当
(舍去)当![]() 时,
时,![]()
因为点![]() 在抛物线上,
在抛物线上,
∴![]()
由题意知![]()
∵![]()
∴当![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,代数式
时,代数式![]() 有最大值4,
有最大值4,
∴![]() 最大值为4.
最大值为4.

【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
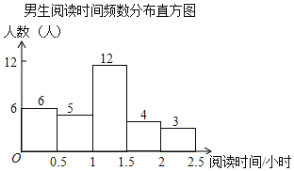
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?