题目内容
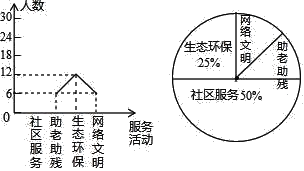
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?

【答案】(1)0.6,4;(2)72,B(比较了解);(3)900人
【解析】
(1)先根据“非常了解”的频数及其频率求得总人数,再由频率=频数÷总数求解可得;
(2)用360°乘以“非常了解”的频率可得圆心角度数,再根据众数的定义进一步求解即可;
(3)总人数乘以样本中“比较了解”的频率即可得.
(1)∵本次调查的总人数为40÷0.2=200(人),
∴m=120÷200=0.6,n=200×0.02=4,
故答案为:0.6,4;
(2)等级为“非常了解”的学生在扇形统计图中所对应的扇形的圆心角的度数为:360°×0.2=72°;
根据表格信息可知,其中B(比较了解)出现次数最多,所以所抽取学生对丁雾霾了解程度的众数是B(比较了解).
故答案为:72,B(比较了解);
(3)1500×0.6=900(人),
答:估计这些学生中“比较了解”人数约为900人.

【题目】某单位需招聘一名技术员,对甲、乙、丙三名候选人进行了笔试和面试两项测试,其成绩如下表所示.根据录用程序,该单位又组织了![]() 名人员对三人进行民主评议,其得票率如扇形图所示,每票
名人员对三人进行民主评议,其得票率如扇形图所示,每票![]() 分(没有弃权票。每人只能投
分(没有弃权票。每人只能投![]() 票)
票)
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
笔试 |
|
|
|
面试 |
|
|
|
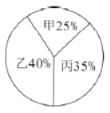
(1)请算出三人的民主评议得分.
(2)该单位将笔试、面试、民主评议三项得分按![]() 确定综合成绩,且民主评议得分低于
确定综合成绩,且民主评议得分低于![]() 分不录取,谁将被录用?请说明理由.
分不录取,谁将被录用?请说明理由.