题目内容
【题目】如图，在平面直角坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C，D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为______.
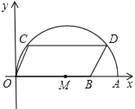
【答案】(1，3)
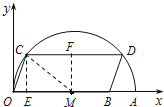
【解析】试题分析：过点M作MF⊥CD于点F，则CF=
CD=4，过点C作CE⊥OA于点E，由勾股定理可求得MF的长，从而得出OE的长，然后写出点C的坐标．
试题解析：∵四边形OCDB是平行四边形，B（8，0），
∴CD∥OA，CD=OB=8
过点M作MF⊥CD于点F，则CF=CD=4
过点C作CE⊥OA于点E，
∵A（10，0），
∴OE=OM-ME=OM-CF=5-4=1．
连接MC，则MC=OA=5
∴在Rt△CMF中，由勾股定理得MF=
∴点C的坐标为（1，3）
练习册系列答案
相关题目
【题目】（答案要求保留小数点后两位数）已知一次考试中某题得分的频数分布表
得分 | 0分 | 1分 | 2分 | 3分 | 4分 | 5分 | 合计 |
频数 | 2 | 4 | 6 | 16 | 8 | 6 | __ |
频率 | __ | __ | __ | __ | __ | __ | __ |
（1）完成上面表格；
（2）该题的平均得分是__；得__分的人数最多，占总人数的__%；
（3）将该题的得分情况制作成扇形统计图．
