题目内容
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
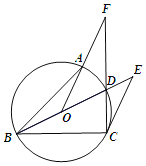
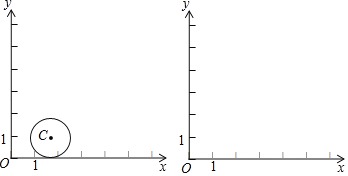
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
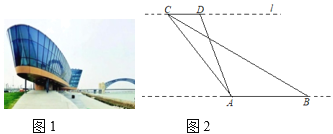
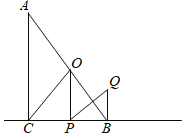
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
【答案】(1)①﹣3;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①把Q(1,a)代入y=x-4,可求出a值,根据理想值定义即可得答案;②由理想值越大,点与原点连线与![]() 轴夹角越大,可得直线
轴夹角越大,可得直线![]() 与
与![]() 相切时理想值最大,
相切时理想值最大,![]() 与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论
与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论![]() 与
与![]() 轴及直线
轴及直线![]() 相切时,LQ 取最小值和最大值,求出
相切时,LQ 取最小值和最大值,求出![]() 点横坐标即可;(3)根据题意将点
点横坐标即可;(3)根据题意将点![]() 转化为直线
转化为直线![]() ,
,![]() 点理想值最大时点
点理想值最大时点![]() 在
在![]() 上,分析图形即可.
上,分析图形即可.
(1)①∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴点![]() 的“理想值”
的“理想值”![]() =-3,
=-3,
故答案为:﹣3.
②当点![]() 在
在![]() 与
与![]() 轴切点时,点
轴切点时,点![]() 的“理想值”最小为0.
的“理想值”最小为0.
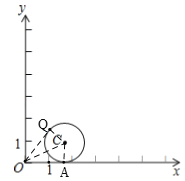
当点![]() 纵坐标与横坐标比值最大时,
纵坐标与横坐标比值最大时,![]() 的“理想值”最大,此时直线
的“理想值”最大,此时直线![]() 与
与![]() 切于点
切于点![]() ,
,
设点Q(x,y),![]() 与x轴切于A,与OQ切于Q,
与x轴切于A,与OQ切于Q,
∵C(![]() ,1),
,1),
∴tan∠COA=![]() =
=![]() ,
,
∴∠COA=30°,
∵OQ、OA是![]() 的切线,
的切线,
∴∠QOA=2∠COA=60°,
∴![]() =tan∠QOA=tan60°=
=tan∠QOA=tan60°=![]() ,
,
∴点![]() 的“理想值”为
的“理想值”为![]() ,
,
故答案为:![]() .
.
(2)设直线与![]() 轴、
轴、![]() 轴的交点分别为点
轴的交点分别为点![]() ,点
,点![]() ,
,
当x=0时,y=3,
当y=0时,![]() x+3=0,解得:x=
x+3=0,解得:x=![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴tan∠OAB=![]() ,
,
∴![]() .
.
∵![]() ,
,
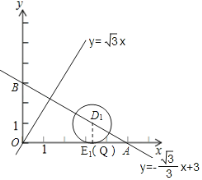
∴①如图,作直线![]() .
.
当![]() 与
与![]() 轴相切时,LQ=0,相应的圆心
轴相切时,LQ=0,相应的圆心![]() 满足题意,其横坐标取到最大值.
满足题意,其横坐标取到最大值.
作![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
②如图
当![]() 与直线
与直线![]() 相切时,LQ=
相切时,LQ=![]() ,相应的圆心
,相应的圆心![]() 满足题意,其横坐标取到最小值.
满足题意,其横坐标取到最小值.
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
∵直线![]() 中,k=
中,k=![]() ,
,
∴![]() ,
,
∴![]() ,点F与Q重合,
,点F与Q重合,
则![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
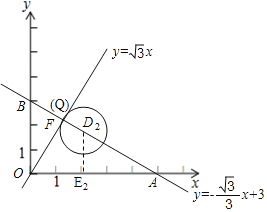
由①②可得,![]() 的取值范围是
的取值范围是![]() .
.
(3)∵M(2,m),
∴M点在直线x=2上,
∵![]() ,
,
∴LQ取最大值时,![]() =
=![]() ,
,
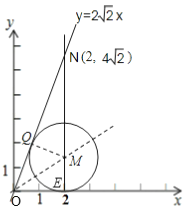
∴作直线y=![]() x,与x=2交于点N,
x,与x=2交于点N,
当![]() M与ON和x轴同时相切时,半径r最大,
M与ON和x轴同时相切时,半径r最大,
根据题意作图如下:![]() M与ON相切于Q,与x轴相切于E,
M与ON相切于Q,与x轴相切于E,
把x=2代入y=![]() x得:y=4
x得:y=4![]() ,
,
∴NE=4![]() ,OE=2,ON=
,OE=2,ON=![]() =6,
=6,
∴∠MQN=∠NEO=90°,
又∵∠ONE=∠MNQ,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:r=![]() .
.
∴最大半径为![]() .
.

【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?

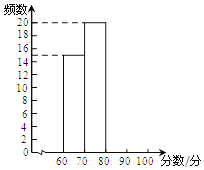
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.