题目内容
【题目】下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线l和直线l外一点A
求作:直线AP,使得AP∥l
作法:如图
①在直线l上任取一点B(AB与l不垂直),以点A为圆心,AB为半径作圆,与直线l交于点C.
②连接AC,AB,延长BA到点D;
③作∠DAC的平分线AP.
所以直线AP就是所求作的直线
根据小星同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
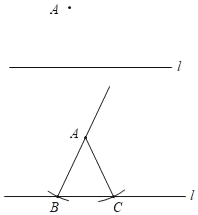
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB (填推理的依据)
∵∠DAC是△ABC的外角,
∴∠DAC=∠ABC+∠ACB (填推理的依据)
∴∠DAC=2∠ABC
∵AP平分∠DAC,
∴∠DAC=2∠DAP
∴∠DAP=∠ABC
∴AP∥l (填推理的依据)
【答案】(1)详见解析;(2)(等边对等角),(三角形外角性质),(同位角相等,两直线平行).
【解析】
(1)根据角平分线的尺规作图即可得;
(2)分别根据等腰三角形的性质、三角形外角的性质和平行线的判定求解可得.
解:(1)如图所示,直线AP即为所求.

(2)证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角),
∵∠DAC是△ABC的外角,
∴∠DAC=∠ABC+∠ACB(三角形外角性质),
∴∠DAC=2∠ABC,
∵AP平分∠DAC,
∴∠DAC=2∠DAP,
∴∠DAP=∠ABC,
∴AP∥l(同位角相等,两直线平行),
故答案为(等边对等角),(三角形外角性质),(同位角相等,两直线平行).

 阅读快车系列答案
阅读快车系列答案【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?

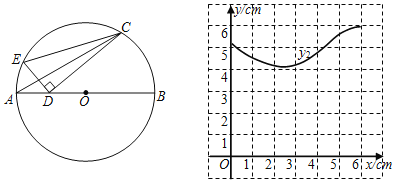
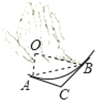
【题目】如图,AB是圆O的直径,点C是圆O上一点,∠CAB=30°,D是直径AB上一动点,连接CD并过点D作CD的垂线,与圆O的其中一个交点记为点E(点E位于直线CD上方或左侧),连接EC.已知AB=6cm,设A、D两点间的距离为xcm,C、D两点间的距离为y1cm,E、C两点间的距离为y2cm,小雪根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小雪的探究过程:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.2 | 4.4 | 3.6 | 3.0 | 2.7 | 2.7 |
|
y2/cm | 5.2 | 4.6 | 4.2 |
| 4.8 | 5.6 | 6.0 |
(1)按照下表中自变量x的值进行取点、面图、测量,分别得到了y1,y2与x的几组对应值,请将表格补充完整:(保留一位小数)
(2)在同一平面直角坐标系xOy中,y2的图象如图所示,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1的图象;
(3)结合函数图象,解决问题:当∠ECD=60°时,AD的长度约为 cm.