题目内容
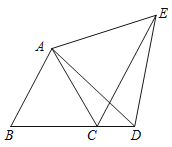
【题目】如图,我市某中学在创建“特色校园”的活动中,将学校的办学理念做成了宣传牌(CD),放置在教学楼的顶部(如图所示),该中学数学活动小组的同学在山坡坡脚A处测得宣传牌底D的仰角为60°,沿坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:![]() ,
,![]() )
)
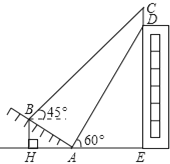
【答案】(1)BH=5 (2)2.7
【解析】分析:(1)在Rt△ABH中,由tan∠BAH=![]() .得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×
.得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×![]() =5;
=5;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,在Rt△ADE中,tan∠DAE=
,在Rt△ADE中,tan∠DAE=![]() ,即tan60°=
,即tan60°=![]() ,得到DE=15
,得到DE=15![]() ,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5
,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5![]() +15,于是得到DF=DE-EF=DE-BH=15
+15,于是得到DF=DE-EF=DE-BH=15![]() -5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5
-5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5![]() +15,即可求得结果.
+15,即可求得结果.
详解:(1)在Rt△ABH中,
∵tan∠BAH=![]() .
.
∴∠BAH=30°,
∴BH=AB.sin∠BAH=10.sin30°=10×![]() =5.
=5.
答:点B距水平面AE的高度BH是5米;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,
,
在Rt△ADE中,tan∠DAE=![]() ,
,
即tan60°=![]() ,∴DE=15
,∴DE=15![]() ,
,
如图,过点B作BF⊥CE,垂足为F,
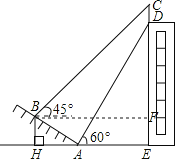
∴BF=AH+AE=5![]() +15,
+15,
DF=DE-EF=DE-BH=15![]() -5,
-5,
在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5![]() +15,
+15,
∴CD=CF-DF=5![]() +15-(15
+15-(15![]() -5)=20-10
-5)=20-10![]() ≈20-10×1.732≈2.7(米),
≈20-10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.