Question

【题目】如图，抛物线y=ax2+bx+3与x轴相交于点A（﹣3，0），B（﹣1，0），与y轴相交于点C，⊙O1为△ABC的外接圆，交抛物线于另一点D．

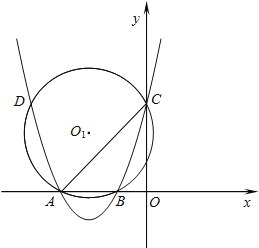
（1）求抛物线的解析式；

（2）求⊙O1的半径．

Answer 1

【答案】（1）y=x2+4x+3；（2）．

【解析】

试题分析：（1）利用待定系数法求出抛物线的解析式；

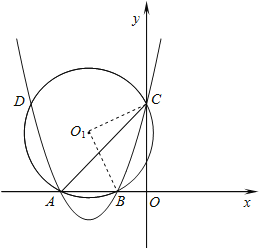
（2）如图所示，由圆周角定理，确定△BO1C为等腰直角三角形，从而求出半径的长度．

解：（1）∵抛物线y=ax2+bx+3与x轴相交于点A（﹣3，0），B（﹣1，0），

∴，

解得a=1，b=4，

∴抛物线的解析式为：y=x2+4x+3；

（2）由（1）知，抛物线解析式为：y=x2+4x+3，

∵令x=0，得y=3，

∴C（0，3），

∴OC=OA=3，则△AOC为等腰直角三角形，

∴∠CAB=45°，

在Rt△BOC中，由勾股定理得：BC==，

如图1所示，连接O1B、O1B，

由圆周角定理得：∠BO1C=2∠BAC=90°，

∴△BO1C为等腰直角三角形，

∴⊙O1的半径O1B=BC=．