题目内容
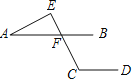
【题目】如图，已知直线AB∥CD，∠C=115°，∠A=25°，则∠E=（ ）
A．70° B．80° C．90° D．100°
【答案】C
【解析】
试题分析：此题的解法灵活，可以首先根据平行线的性质求得∠EFB，再根据三角形的外角性质求得∠E；也可以首先根据平行线的性质求得∠CFB，再根据对顶角相等求得∠AFE，最后再根据三角形的内角和定理即可求解．
解：方法1：
∵AB∥CD，∠C=115°，
∴∠EFB=∠C=115°．
又∠EFB=∠A+∠E，∠A=25°，
∴∠E=∠EFB﹣∠A=115°﹣25°=90°；
方法2：
∵AB∥CD，∠C=115°，
∴∠CFB=180°﹣115°=65°．
∴∠AFE=∠CFB=65°．
在△AEF中，∠E=180°﹣∠A﹣∠AEF=180°﹣25°﹣65°=90°．
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
