Question

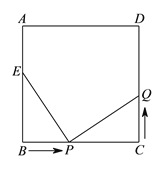
【题目】已知：如图，正方形ABCD的边长为10 cm，点E在边AB上，且AE=4 cm，点P在线段BC上以每秒2 cm的速度由点B向点C运动，同时点Q在线段CD上由点C向点D运动．设点P运动时间为t秒，若某一时刻△BPE与△CQP全等，求此时t的值及点Q的运动速度．

Answer 1

【答案】当t=2，Q的速度为每秒2cm或t=，Q的速度为每秒cm时，△BEP与△CQP全等．

【解析】试题分析：分△BEP≌△CPQ， △BEP≌△CQP，两种情况进行讨论即可得.

试题解析：由题意得BP=2t，

∵正方形ABCD的边长为10cm，∴AB=BC=10，∴PC=10-2t，

∵AE=4 cm，∴BE=10-4 =6（cm），

①要使△BEP≌△CPQ，则需EB=PC，BP=CQ，即6=10-2t，CQ=2t，∴t=2，CQ=4，

则点Q的速度为===2（cm/s），

即当t=2 秒，Q的速度为每秒2cm时，△BEP≌△CPQ；

②要使△BEP≌△CQP，则需BP=CP，BE=CQ，即2t=10-2t，CQ=6，∴t=，

则点Q的速度为==6×=（cm/s），

即当t=秒，Q的速度为每秒cm时，△BEP≌△CQP；

综上所述，当t=2秒，Q的速度为每秒2cm或t=，Q的速度为每秒cm时，△BEP与△CQP全等．