Question

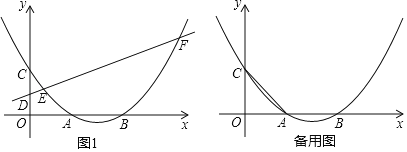
【题目】如图，抛物线与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C（0，3）.

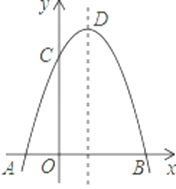
（1）求此抛物线所对应函数的表达式；

（2）若M 是抛物线对称轴上一个动点，求当 MA+MC 的值最小时 M 点坐标；

（3）若抛物线的顶点为D，在其对称轴右侧的抛物线上是否存在点P，使得△PCD为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由.

Answer 1

【答案】（1） ；（2）M(1，2) ；（3）存在P点坐标为或（2，3），理由见解析

【解析】

（1）根据A、B的坐标设抛物线饿表达式是y＝a（x＋1）（x3），把C的坐标代入求出a，即可得出答案；

（2）根据点A关于对称轴的对称点为B，连接BC，直线BC与对称轴的交点即为所求的点M．

（3）求出D的坐标和对称轴的表达式，分为两种情况：①若以CD为底边，则PC＝PD．设P点坐标为（a，b），根据勾股定理求出b＝4a，代入抛物线求出a、b，②若以CD为一腰，根据抛物线对称性得出点P与点C关于直线x＝1对称，即可求出P的坐标．

（1）设表达式为 ，

抛物线与x轴交于点（﹣1，0）和（3，0），又点（0，3）在抛物线上，

则 ，

故所求的表达式为：

即

（2）由=知，

D点坐标为（1，4），对称轴为x=1

由题意得：点A关于对称轴x=1的对称点为点B，

连接CB交对称轴为x=1于点M

设直线CB解析式为y=kx+b,∵C（0，3）B（3，0）

∴直线CB解析式为y=-x+3

又∵对称轴为x=1

∴

∴

∴M(1，2)即为所求.

（3）存在，

由=知，

D点坐标为（1，4），对称轴为x=1

①以CD为底边，则PC=PD

设P点坐标为

由勾股定理，得：

即．

又点P在抛物线上，∴，

∴

整理得:

解之得 ， （不合题意，舍去）

∴ ，

∴，

P

②若以CD为一腰，因点P在对称轴右侧的抛物线上，

由抛物线对称性知，点P与点C关于直线x=1对称，

此时点P坐标为（2，3）

综上所述，符合条件的点P坐标为或（2，3）