题目内容
【题目】在平面直角坐标系xOy中,点A(0,2),抛物线y=mx2+4mx+5m的对称轴与x轴交于点B.
(1)求点B的坐标;
(2)当m>0时,过A点作直线l平行于x轴,与抛物线交于C、D两点(C在D左侧),C、D横坐标分别为x1、x2,且x2﹣x1=2,求抛物线的解析式;
(3)若抛物线与线段AB恰只有一个公共点,则请结合函数图象,直接写出m的取值范围.
【答案】(1)(﹣2,0);(2) y=x2+4x+5;(3) 0<m<![]() 或m=
或m=![]() .
.
【解析】
(1)利用对称轴公式求得对称轴,即可求得B的坐标;
(2)先根据对称轴求出x1+x2=﹣4,结合x2﹣x1=2,即可求出x1和x2的值,从而可求出C(﹣3,2),D(﹣1,2),然后用待定系数法求解即可;
(3)当m<0时不合题意;当m>0,分两种情况讨论,结合图象即可求得.
解:(1)∵抛物线y=mx2+4mx+5m的对称轴为直线x=﹣![]() =﹣2,
=﹣2,
∴对称轴与x轴交点B的坐标为(﹣2,0);
(2)由题意可知,C、D两点关于抛物线的对称轴对称,且C在D的左边,
∴![]() =﹣2,
=﹣2,
∴x1+x2=﹣4,
∵x2﹣x1=2,
∴x1=﹣3,x2=﹣1,
∵A(0,2),且过A的直线l平行于x轴,
∴C(﹣3,2),D(﹣1,2),
将D点代入抛物线,得m﹣4m+5m=2,
解,得m=1,
∴抛物线的解析式为y=x2+4x+5;
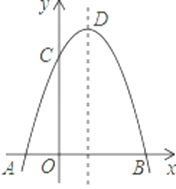
(3)∵A(0,2),B(﹣2,0),
∴线段AB在x轴上方,直线AB=x+2,
函数y=mx2+4mx+5m中,△=(4m)2﹣4m5m=﹣4m2<0,
∴抛物线与x轴无交点,
当m<0时,抛物线开口向下,顶点在x轴下方,与线段AB为交点,
当m>0时,抛物线开口向上,顶点在x轴上方,若抛物线与AB有一个交点,有两种情况:
①如图1,抛物线与AB相切时,则mx2+4mx+5m=x+2整理得,mx2+(4m﹣1)x+5m﹣2=0,
△=(4m﹣1)2﹣4m(5m﹣2)=0,解得m=![]() 或m=﹣
或m=﹣![]() (舍去),
(舍去),
②抛物线与y轴的交点在O、A之间,即0<5m<2,解得0<m<![]() ,
,
综上所述,m的取值范围是 0<m<![]() 或m=
或m=![]() .
.


 名校课堂系列答案
名校课堂系列答案