题目内容
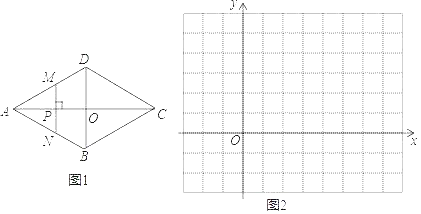
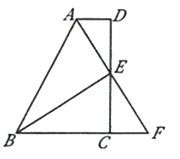
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,且
,且![]() 平分
平分![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() 是
是![]() 的平分线;
的平分线;
(4)探究![]() 和
和![]() 的面积间的数量关系,并写出探究过程.
的面积间的数量关系,并写出探究过程.
【答案】(1)详见解析;(2)详见解析;(3)详见解析;(4)![]() ;详见解析
;详见解析
【解析】
(1)根据AAS证明![]() ,再由全等三角形的性质得到结论;
,再由全等三角形的性质得到结论;
(2)先证明![]() 得到△ABF是等腰三角形,从而证明
得到△ABF是等腰三角形,从而证明![]() ,再根据
,再根据![]() 得到结论;
得到结论;
(3)先证明AE=EF,再结合△ABF是等腰三角形,根据三线合一得到结论;
(4)根据三线合一可得S△ABE=S△BEF,再根据S△BEF=S△BCE+S△CEF和![]() 得到结论.
得到结论.
(1)证明:∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
在![]() 和
和![]() 中
中
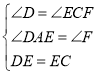 ,
,
∴![]() ,
,
∴![]() ;
;
(2)证明:∵![]() 平分
平分![]() ,
,
∴![]() ,
,
由(1)知![]() ,
,
∴![]() ,
,
∴△ABF是等腰三角形,
∴![]()
由(1)知![]() ,
,
∴![]() ;
;
(3)证明:由(1)知![]() ,
,
∴![]() ,
,
由(2)知![]() ,
,
∴![]() 是等腰
是等腰![]() 底边上的中线,
底边上的中线,
∴![]() 是
是![]() 的平分线;
的平分线;
(4)∵△ABF是等腰三角形,BE是中线,(已证)
∴S△ABE=S△BEF,
又∵S△BEF=S△BCE+S△CEF,![]() (已证),
(已证),
∴S△BEF=S△BCE+S△ADE,
∴![]() .
.

练习册系列答案
相关题目