题目内容
【题目】问题情境：课堂上，同学们研究几何变量之间的函数关系问题：如图，菱形ABCD的对角线AC，BD相交于点O，AC=4，BD=2．点P是AC上的一个动点，过点P作MN⊥AC，垂足为点P（点M在边AD、DC上，点N在边AB、BC上）．设AP的长为x（0≤x≤4），△AMN的面积为y．
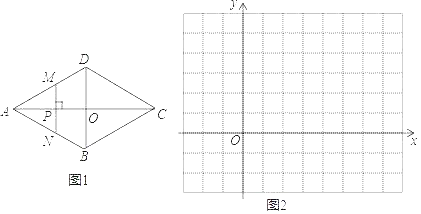
建立模型：（1）y与x的函数关系式为：
，
解决问题：（2）为进一步研究y随x变化的规律，小明想画出此函数的图象．请你补充列表，并在如图的坐标系中画出此函数的图象：
x | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y | 0 |
|
|
|
|
|
|
| 0 |
（3）观察所画的图象，写出该函数的两条性质： ．
【答案】(1) ①y=
;②
;(2)见解析；（3）见解析
【解析】
（1）根据线段相似的关系得出函数关系式（2）代入①中函数表达式即可填表（3）画图像，分析即可.
（1）设AP=x
①当0≤x≤2时
∵MN∥BD
∴△APM∽△AOD
∴
∴MP=
∵AC垂直平分MN
∴PN=PM=
x
∴MN=x
∴y=APMN=
②当2＜x≤4时，P在线段OC上，
∴CP=4﹣x
∴△CPM∽△COD
∴
∴PM=
∴MN=2PM=4﹣x
∴y=
=﹣
∴y=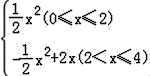
（2）由（1）
当x=1时，y=
当x=2时，y=2
当x=3时，y=
（3）根据（1）画出函数图象示意图可知
1、当0≤x≤2时，y随x的增大而增大
2、当2＜x≤4时，y随x的增大而减小
练习册系列答案
名校课堂系列答案
相关题目
