题目内容
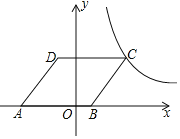
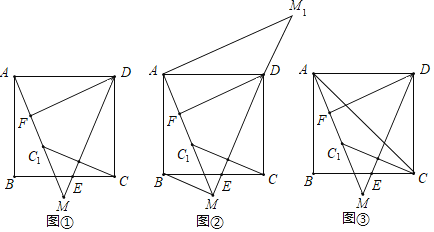
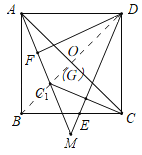
【题目】如图,在正方形ABCD中,点E是边BC上任意一点(点E不与点B、C重合),连结DE,点C关于DE的对称点为C1,连结AC1并延长交DE的延长线于点M,F是AC1的中点,连结DF.
(猜想)如图①,∠FDM的大小为 度.
(探究)如图②,过点A作AM1∥DF交MD的延长线于点M1,连结BM.求证:△ABM≌△ADM1.
(拓展)如图③,连结AC,若正方形ABCD的边长为2,则△ACC1面积的最大值为 .
【答案】(1)45°;(2)证明见解析;(3)2![]() ﹣2.
﹣2.
【解析】
(1)证明∠CDE=∠C1DE和∠ADF=∠C1DF,可得∠FDM=![]() ∠ADC=45°;
∠ADC=45°;
(2)先判断出∠DAM1=∠BAM,由(1)可知:∠FDM=45°,进而判断出∠AMD=45°,得出AM=AM1,即可得出结论;
(3)先作高线C1G,确定△ACC1的面积中底边AC为定值2,根据高的大小确定面积的大小,当C1在BD上时,C1G最大,其△AC1C的面积最大,并求此时的面积.
(1)由对称得:CD=C1D,∠CDE=∠C1DE,
在正方形ABCD中,AD=CD,∠ADC=90°,
∴AD=C1D,
∵F是AC1的中点,
∴DF⊥AC1,∠ADF=∠C1DF,
∴∠FDM=∠FDC1+∠EDC1=![]() ∠ADC=45°;
∠ADC=45°;
故答案为:45;
(2)∵DF⊥AC1,
∴∠DFM=90°,
∵AM1∥DF
∴∠MAM'=90°,
在正方形ABCD中,DA=BA,∠BAD=90°,
∴∠DAM1=∠BAM,
由(1)可知:∠FDM=45°
∵∠DFM=90°
∴∠AMD=45°,
∴∠M1=45°,
∴AM=AM1,
在:△ABM和△ADM1中,
∵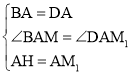 ,
,
∴△ABM≌△ADM1(SAS);
(3)如图,过C1作C1G⊥AC于G,则![]() =
=![]() ACC1G,
ACC1G,
在Rt△ABC中,AB=BC=2,
∴AC=![]() =2
=2![]() ,即AC为定值,
,即AC为定值,
当C1G最大值,△AC1C的面积最大,
连接BD交AC于O,当C1在BD上时,C1G最大,此时G与O重合,
∵CD=C1D=2,OD=![]() AC=
AC=![]() ,
,
∴C1G=C1D﹣OD=2﹣![]() ,
,
∴![]() =
=![]() ACC1G=
ACC1G=![]() ×2
×2![]() (2﹣
(2﹣![]() )=2
)=2![]() ﹣2,
﹣2,
故答案为:2![]() ﹣2.
﹣2.