题目内容
【题目】正比例函数y=x的图象与反比例函数y=![]() 的图象有一个交点的纵坐标是﹣2.
的图象有一个交点的纵坐标是﹣2.
(1)当x=3时,求反比例函数y=![]() 的值;
的值;
(2)当﹣3<x<﹣1时,求反比例函数y=![]() 的取值范围;
的取值范围;
(3)请直接写出关于x的不等式x<![]() <0的解集.
<0的解集.
【答案】(1)![]() ;(2)当﹣3<x<﹣1时,
;(2)当﹣3<x<﹣1时,![]() ;(3)x<﹣2.
;(3)x<﹣2.
【解析】
(1)首先把![]() 代入直线的解析式,求得交点坐标,然后用待定系数法求得反比例函数的解析式,再把
代入直线的解析式,求得交点坐标,然后用待定系数法求得反比例函数的解析式,再把![]() 代入求值;
代入求值;
(2)先求得当![]() 和
和![]() 时
时![]() 的值,然后根据反比例函数的性质求解.
的值,然后根据反比例函数的性质求解.
(3)根据两个函数的图象及它们的交点坐标即可求得.
(1)把y=2代入y=x,得x=2,
把x=2,y=2代入![]() ,得
,得![]() ,解得k=4,
,解得k=4,
∴反比例函数的解析式为![]() ,
,
当x=3时![]() =
=![]() .
.
(2)当x=﹣3时,![]() =-
=-![]() ,
,
当x=﹣1时,![]() =-4,
=-4,
因为k=4>0,所以当﹣3<x<﹣1时,![]() 中y随x的增大而减小,
中y随x的增大而减小,
所以当﹣3<x<﹣1时,![]() .
.
(3)由图象可知:正比例函数y=x的值小于反比例函数![]() 的值的
的值的![]() 取值范围是:
取值范围是:![]() 或
或![]() ,
,
∴不等式x<![]() <0的解集是:x<﹣2.
<0的解集是:x<﹣2.

练习册系列答案
相关题目
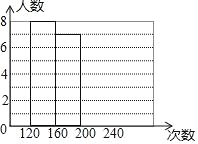
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?