题目内容
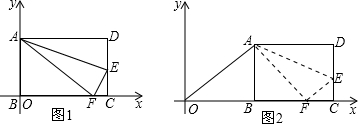
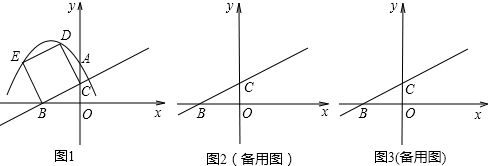
如图1,在直角坐标系中放入一个边长AB长为6,BC长为10的矩形纸片ABCD,B点与坐标原点O重合.将纸片沿着折痕AE翻折后,点D恰好落在x轴上,记为F.
(1)求折痕AE所在直线与x轴交点的坐标;
(2)求过D,F的直线解析式;
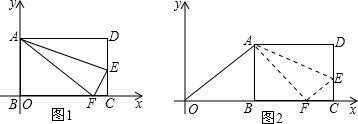
(3)将矩形ABCD水平向右移动m个单位,则点B坐标为(m,0),其中m>0.如图2所示,连接OA,若△OAF是等腰三角形,求m的值.
 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,∴AD=CB=10,AB=DC=6,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=10,EF=DE,
在Rt△ABF中,BF=
 =
=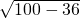 =8,
=8,∴CF=2,
设EC=x,则EF=6-x,
在Rt△ECF中,22+x2=(6-x)2,
解得:x=
 ,
,∴E点坐标为:(10,
 ),
),∴设AE所在直线解析式为:y=ax+b,
则
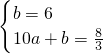 ,
,解得:
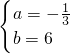 ,
,∴AE所在直线解析式为:y=-
 x+6,
x+6,当y=0时,x=18,
故折痕AE所在直线与x轴交点的坐标为:(18,0);
(2)设D,F所在直线解析式为:y=kx+c,
∵BF=8,∴F点坐标为:(8,0),
将D,F点坐标代入解析式得:
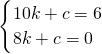 ,
,解得:
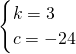 ,
,∴过D,F的直线解析式为:y=3x-24;
(3)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=8,
∴m=8,
若OF=FA,则m+8=10,
解得:m=2,
若AO=OF,在Rt△AOB中,
AO2=OB2+AB2=m2+36,
∴(m+8)2=m2+36,
解得:m=-
 (m<0不合题意舍去),
(m<0不合题意舍去),综上所述,若△OAF是等腰三角形,m的值为m=8或2.
分析:(1)根据四边形ABCD是矩形以及由折叠对称性得出AF=AD=10,EF=DE,进而求出BF的长,即可得出E点的坐标,进而得出AE所在直线与x轴交点的坐标;
(2)由(1)中所求可得出F点坐标,进而得出过D,F的直线解析式;
(3)分三种情况讨论:若AO=AF,OF=FA,AO=OF,利用勾股定理求出即可.
点评:此题主要考查了一次函数的综合应用以及翻折变换的性质和勾股定理等知识,一次函数的综合应用是初中阶段的重点题型特别注意利用数形结合以及分类讨论思想是这部分考查的重点也是难点同学们应重点掌握.

练习册系列答案
相关题目
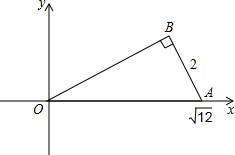 已知在Rt△OAB中,∠B=90°,
已知在Rt△OAB中,∠B=90°,
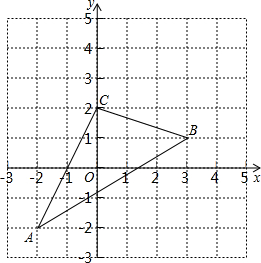 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,