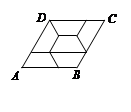题目内容
由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1,B2,B3,…,Bn和C1,C2,C3,…,Cn分别在直线 和x轴上,则第一个阴影正方形的面积为 ▲ ,第n个阴影正方形的面积为 ▲ .
和x轴上,则第一个阴影正方形的面积为 ▲ ,第n个阴影正方形的面积为 ▲ .
 和x轴上,则第一个阴影正方形的面积为 ▲ ,第n个阴影正方形的面积为 ▲ .
和x轴上,则第一个阴影正方形的面积为 ▲ ,第n个阴影正方形的面积为 ▲ .
 ,
,
解:因为由题意可知,全等的直角三角形有一个角为30°则斜边为其对应直角边的二倍,
令OC1=1,则B1C1="1," P1C1="1/2," 顶点B1,B2,B3,…,Bn和C1,C2,C3,…,Cn分别在直线 和x轴上,而第一个阴影部分的正方形的边长为直角边的差,得到其面积,同理依次得到第二个正方形边长为第一个正方形边长的2/3,依次类推,得到第n个阴影正方形的面积。
和x轴上,而第一个阴影部分的正方形的边长为直角边的差,得到其面积,同理依次得到第二个正方形边长为第一个正方形边长的2/3,依次类推,得到第n个阴影正方形的面积。
令OC1=1,则B1C1="1," P1C1="1/2," 顶点B1,B2,B3,…,Bn和C1,C2,C3,…,Cn分别在直线
 和x轴上,而第一个阴影部分的正方形的边长为直角边的差,得到其面积,同理依次得到第二个正方形边长为第一个正方形边长的2/3,依次类推,得到第n个阴影正方形的面积。
和x轴上,而第一个阴影部分的正方形的边长为直角边的差,得到其面积,同理依次得到第二个正方形边长为第一个正方形边长的2/3,依次类推,得到第n个阴影正方形的面积。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 AFE是等腰三角形 ;(2)AF=BM.
AFE是等腰三角形 ;(2)AF=BM.