题目内容
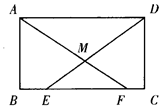
已知：如图，∠1=∠2，E是AD上一点，且BE∥MF，EF∥AB．求证：
（1）
AFE是等腰三角形 ；（2）AF=BM．
（1）
AFE是等腰三角形 ；（2）AF=BM．证明见解析
解：（1）
EF∥AB，
，-----------------------------（1分）
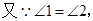
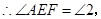……………………………(2分)
，
是等腰三角形.…………………（4分）
(2)BE∥MF,EF∥AB,
四边形BEFM是平行四边形, ……………………………………（6分）
BM="EF,"
AF=BM. ……………………………………（8分）
（1）由EF∥AB，得出∠AEF=∠1，通过∠1=∠2，得出∠AEF=∠2，从而得出结论
(2)由BE∥MF，EF∥AB，可判断四边形BMEF为平行四边形，再根据同位角求出∠2=∠AEF，即可得出结论．
EF∥AB，，-----------------------------（1分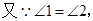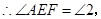）……………………………(2分)，是等腰三角形.…………………（4分）(2)
BE∥MF,EF∥AB,四边形BEFM是平行四边形, ……………………………………（6分）BM="EF," AF=BM. ……………………………………（8分）（1）由EF∥AB，得出∠AEF=∠1，通过∠1=∠2，得出∠AEF=∠2，从而得出结论
(2)由BE∥MF，EF∥AB，可判断四边形BMEF为平行四边形，再根据同位角求出∠2=∠AEF，即可得出结论．
练习册系列答案
相关题目
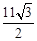
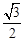
和x轴上，则第一个阴影正方形的面积为 ▲ ，第n个阴影正方形的面积为 ▲ .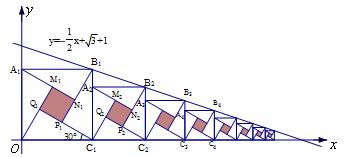
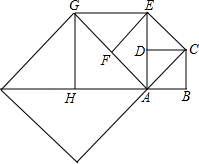
ABCD中, ∠C=90度，沿着直线BD折叠，使点C落在
处，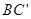
交AD于E，
，
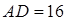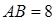，求DE的长．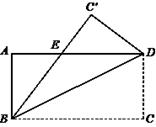
是平行四边形，
于
，
于
.求证：
.