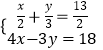��Ŀ����
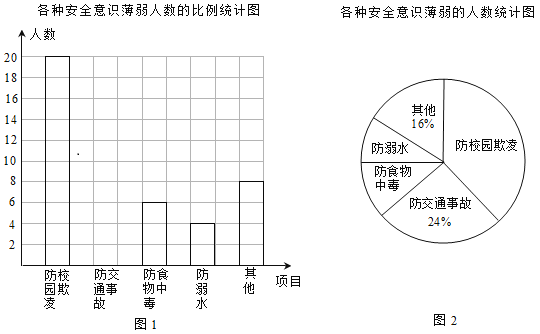
����Ŀ����������ͼ�������ʡ���չѧϰƬ��չʾ��
�����⡿��ͼ������ƽ��ֱ������ϵ�У�������y=a��x��2��2��![]() ����ԭ��O����x�����һ������ΪA����a= ��
����ԭ��O����x�����һ������ΪA����a= ��
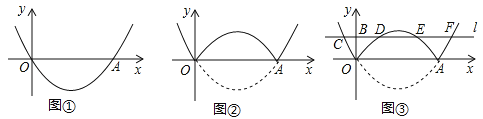
����������ͼ������������x���·��IJ�����x���۵���x���Ϸ������ⲿ��ͼ����ԭ������ʣ�ಿ�ֵ�ͼ����ɵ���ͼ���ΪG����ͼ����ֱ��д��ͼ��G��Ӧ�ĺ�������ʽ��
��̽������ͼ���У�����B��0��1����ֱ��lƽ����x�ᣬ��ͼ��G�Ľ��������������Ϊ��C��D��E��F����ͼ������ͼ��G��ֱ��l�Ϸ��IJ��ֶ�Ӧ�ĺ���y��x���������ʱx��ȡֵ��Χ��
��Ӧ�á�P��ͼ����ͼ��G��һ�㣬�������Ϊm������PD��PE��ֱ��д����PDE�������С��1ʱm��ȡֵ��Χ��
���𰸡������⡿��a=![]() ������������y=
������������y= ����̽��������1��x��2��x��2+
����̽��������1��x��2��x��2+![]() ʱ������y��x���������Ӧ�á���m=0��m=4��m��2��
ʱ������y��x���������Ӧ�á���m=0��m=4��m��2��![]() ��m��2+
��m��2+![]() ��
��
��������
��������������⡿���ѣ�0��0����������a��ֵ��
������������д����x���۵������������ߵĽ���ʽ������ͼ��ɵö�Ӧȡֵ�Ľ���ʽ��
��̽��������y=0���ֱ�������������ߵĽ���ʽ���ֱ�����ĸ���CDEF�����꣬����ͼ����������ƵIJ��֣���y��x���������д��x��ȡֵ��
��Ӧ�á�������DE�ij������������������ߵ�ȡֵh��1��
�������ֽ������ۣ�
����P��C������F���Ҳಿ��ʱ����P[m��![]() ]������h��1���в���ʽ������ɣ�
]������h��1���в���ʽ������ɣ�
����ͼ�������Գ�����������С��1��֪����P��������DE���Ϸ���
��P��O��A�غ�ʱ������������m=0��m=4��
��������������⡿
��������y=a��x��2��2��![]() ����ԭ��O��
����ԭ��O��
��0=a��0��2��2��![]() ��
��
a=![]() ��
��
������������ͼ���������ߣ�y=![]() ��x��2��2��
��x��2��2��![]() ��
��
�Գ����ǣ�ֱ��x=2���ɶԳ��Եã�A��4��0����
��x���۵�������������Ϊ��y=��![]() ��x��2��2+
��x��2��2+![]()
��ͼ����ͼ��G��Ӧ�ĺ�������ʽΪ��y= ��
��
��̽��������ͼ����������ã�
��y=1ʱ��![]() ��x��2��2��
��x��2��2��![]() =0��
=0��
��ã�x1=2+![]() ��x2=2��
��x2=2��![]() ��
��
��C��2��![]() ��1����F��2+
��1����F��2+![]() ��1����
��1����
��y=1ʱ����![]() ��x��2��2+
��x��2��2+![]() =0��
=0��
��ã�x1=3��x2=1��
��D��1��1����E��3��1����
��ͼ��ã�ͼ��G��ֱ��l�Ϸ��IJ��֣���1��x��2��x��2+![]() ʱ������y��x���������
ʱ������y��x���������
��Ӧ�á�����D��1��1����E��3��1����
��DE=3��1=2��
��S��PDE= ![]() DEh��1��
DEh��1��
��h��1��
����P��C������F���Ҳಿ��ʱ����P[m��![]() ]��
]��
��h=![]() ��m��2��2��
��m��2��2��![]() ��1��1��
��1��1��
��m��2��2��10��
m��2��![]() ��m��2����
��m��2����![]() ��
��
m��2+![]() ��m��2��
��m��2��![]() ��
��
����ͼ�������Գ��ύ������G��H����ֱ��CD��M����x����N��
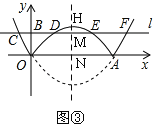
��H��2��![]() ����
����
��HM=![]() ��1=
��1=![]() ��1��
��1��
������P��������DE���Ϸ���
�ۡ�MN=1��
��O��0��0����a��4��0����
��P��O��A�غ�ʱ������������
��m=0��m=4��
������������PDE�������С��1ʱ��m��ȡֵ��Χ�ǣ�m=0��m=4��m��2��![]() ��m��2+
��m��2+![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�