Question

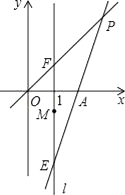
【题目】如图，直线PA是一次函数y=x+1的图象，直线PB是一次函数y=﹣2x+2的图象．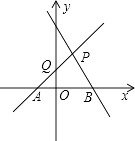

（1）求A、B、P三点的坐标；
（2）求四边形PQOB的面积．

Answer 1

【答案】
（1）解：∵一次函数y=x+1的图象与x轴交于点A，∴A（﹣1，0），

一次函数y=﹣2x+2的图象与x轴交于点B，∴B（1，0），

由 ，解得 ，∴P（ ， ）．

（2）解：设直线PA与y轴交于点Q，则Q（0，1），直线PB与y轴交于点M，则M（0，2），

∴四边形PQOB的面积=S△BOM﹣S△QPM= ×1×2﹣ ×1× =

【解析】（1）两条直线与x轴相交，y为0，得出两个一元一次方程，求出x的值，则可写出A、B两点的坐标，p为两条直线的交点，解这个二元一次方程组，可得p点的坐标。
（2）设直线PB与y轴交于M点。四边形PQOB的构成是由三角形BOM-三角形PQM得到的。