题目内容
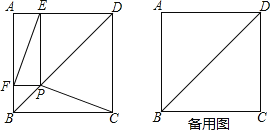
【题目】如图，P是正方形ABCD对角线BD上的一动点
不与B、D重合
，
，
，垂足分别为E、F．
求证：四边形AFPE为矩形；
求证：
；
当EF取最小值时，判断四边形APEF是怎样的四边形？证明你的结论．
【答案】（1）详见解析；（2）详见解析；（3）详见解析.
【解析】
(1)由三个角是直角的四边形是矩形可判断四边形AFPE为矩形；
(2)由矩形的性质和正方形的性质可得AP=CP=EF；
(3)当AP⊥BD时，EF取最小值，由正方形的性质可得AB=AD，∠BAD=90°，由等腰三角形的性质和角平分线的性质可得PE=PF，可得四边形AFPE是正方形．
四边形ABCD是正方形，
，且
，
，
四边形AFPE为矩形；
如图，连接AC，AP，
四边形ABCD是正方形，
垂直平分AC，
，
四边形AFPE为矩形，
，
；
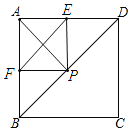
四边形AFPE是正方形，理由如下：
如图，当
时，EF取最小值，
四边形ABCD是正方形，
，
，
又
，
，且，，
，且四边形AFPE是矩形，
四边形AFPE是正方形.
练习册系列答案
相关题目
