题目内容
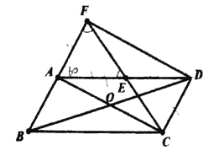
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：
①ac＜0②2a+b=0③4a+2b+c＞0④对任意实数x均有ax2+bx≥a+b
正确的结论序号为：______ ．
【答案】①②④
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
∵抛物线开口向上，
∴a＞0，
∵抛物线与y轴的交点在x轴的下方，
∴c＜0，
∴ac＜0，故①正确．
∵对称轴x=﹣
=1，
∴2a=﹣b，
∴b+2a=0，故②正确；
根据图象知道
当x=2时，y=4a+2b+c＜0，故③错误，
∵当x=1时，y最小=a+b+c，
∴ax2+bx+c≥a+b+c，
∴ax2+bx≥a+b，故④正确．
∴正确的结论序号为：①②④，
故答案为：①②④．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A、B两仓库．已知甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨．从甲、乙两库到A、B两库的路程和运费如下表：（表中“元/吨千米”表示每吨粮食运送1千米所需人民币）
路程（千米） | 运费（元/吨千米） | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
