Question

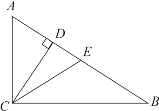
【题目】如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD、CE分别是△ABC的高和中线，下列说法错误的是( )

A.AD =ABB.S△CEB = S△ACE

C.AC、BC的垂直平分线都经过ED.图中只有一个等腰三角形

Answer 1

【答案】D

【解析】

根据含30°的直角三角形、直角三角形斜边上的中线及等边三角形的性质即可依次判断.

∵Rt△ACB中，∠ACB=90°，∠A=60°，CE是△ABC的中线，

∴AE=CE=BE，∴AC、BC的垂直平分线都经过E，C正确；

∴△AEC为等边三角形，∵CD⊥AB，∴AD=DE=AE=AB，A正确；

∵CE是△ABC的中线，∴S△CEB = S△ACE，正确；

图中等腰三角形有△AEC和△BCE，故D错误；

故选D.