题目内容
【题目】如图,在平面直角坐标系中,已知点A的坐标是(a,0),点B的坐标是(b,0),其中a,b满足![]() .
.
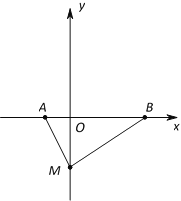
(1)填空:a=______,b=_______;
(2)在![]() 轴负半轴上有一点M(0,m),三角形ABM的面积为4.
轴负半轴上有一点M(0,m),三角形ABM的面积为4.
①求m的值;
②将线段AM沿x轴正方向平移,使得A的对应点为B,M的对应点为N. 若点P为线段AB上的任意一点(不与A,B重合),试写出∠MPN,∠PMA,∠PNB之间的数量关系,并说明理由.
【答案】(1)-1、3;(2)①m=-2,②见解析.
【解析】
(1)根据平方根和平方大于等于零,可求得a、b.
(2)①根据三角形的面积公式,可求得m. ②根据平行线的性质,适当作辅助线,可求得三个角的梳理关系.
(1)由a,b满足![]() ,可得
,可得![]() ,则
,则![]() .
.
(2)①M在![]() 轴负半轴上,则三角形ABM的面积为
轴负半轴上,则三角形ABM的面积为![]() ,则m=-2.
,则m=-2.
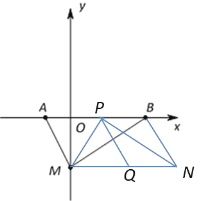
②根据题意,如下图所示,![]() .
.
过点P作![]() 交MN于点Q,根据两直线平行,内错角相等,可得∠PMA=∠QPM,∠PNB=∠QPN,则∠PMA+∠PNB=∠QPM+∠QPN=∠MPN,即∠MPN,∠PMA,∠PNB之间的数量关系为∠PMA+∠PNB=∠MPN.
交MN于点Q,根据两直线平行,内错角相等,可得∠PMA=∠QPM,∠PNB=∠QPN,则∠PMA+∠PNB=∠QPM+∠QPN=∠MPN,即∠MPN,∠PMA,∠PNB之间的数量关系为∠PMA+∠PNB=∠MPN.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/ | -20 | -10 | 0 | 10 | 20 | 30 |
声速/( | 318 | 324 | 330 | 336 | 342 | 348 |
下列说法中错误的是( )
A.在这个变化过程中,当温度为10![]() 时,声速是336
时,声速是336![]()
B.温度越高,声速越快
C.当空气温度为20![]() 时,声音5
时,声音5![]() 可以传播1740
可以传播1740![]()
D.当温度每升高10![]() ,声速增加6
,声速增加6![]()