题目内容
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
【答案】(1)年利润W(万元)关于售价x(元/件)的函数解析式为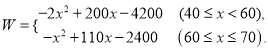 ;
;
(2)当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元;
(3)要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
【解析】(1)根据:年利润=(售价﹣成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案;
(3)根据题意知W≥750,可列关于x的不等式,求解可得x的范围.
解:(1) 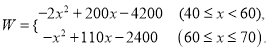
(2)由(1)知,当40≤x<60时, ![]() .
.
∵-2<0,∴当x=50时,W有最大值800.
当60≤x≤70时, ![]() .
.
∵-1<0, ∴当60≤x≤70时,W随x的增大而减小.
∴当x=60时,W有最大值600.
![]()
∴当该产品的售价定为50元/件时,销售该产品的年利润最大,最大利润为800万元.
(3)当40≤x<60时,令W=750,得
-2(x-50)2+800=750,解之,得![]()
由函数![]() 的性质可知,
的性质可知,
当45≤x≤55时,W≥750.
当60≤x≤70时,W最大值为600<750.
所以,要使企业销售该产品的年利润不少于750万元,该产品的销售价x(元/件)的取值范围为45≤x≤55.
“点睛”本题主要考查二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.