题目内容
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
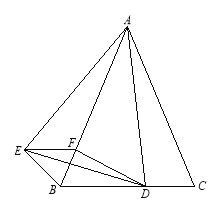
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
【答案】见解析
【解析】
试题分析:根据旋转可得AE=AD,AB=AC,∠EAD=∠BAC,从而得到∠BAE=∠CAD,从而得出△ACD和△ABE全等,从而得出答案;根据题意得出△ABD和△ABE全等,从而得出∠EBF=∠DBF,根据EF∥BC得到∠DBF=∠EFB,从而得到∠EBF=∠EFB,则EB=EF,利用同理得出BD=FD,从而得到菱形.
试题解析:(1)∵△ABC是等腰三角形,顶角∠BAC=α(α<60°),线段AD绕点A顺时针旋转α到AE,∴AE=AD,AB=AC,∠EAD=∠BAC, ∴∠BAE=∠CAD
在△ACD和△ABE中 ∴△ACD≌△ABE(SAS) ∴BE=CD;
∴△ACD≌△ABE(SAS) ∴BE=CD;
(2)∵AD⊥BC,∴BD=CD,∠BAD=∠CAD, 由(1)可知,△ACD≌△ABE,∴BE=BD=CD,∠BAE=∠BAD
在△ABD和△ABE中,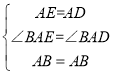 ∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∴△ABD≌△ABE(SAS), ∴∠EBF=∠DBF,
∵EF∥BC, ∴∠DBF=∠EFB, ∴∠EBF=∠EFB, ∴EB=EF,同理BD=FD,∴BD=BE=EF=FD,
∴四边形BDFE为菱形

【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/ | -20 | -10 | 0 | 10 | 20 | 30 |
声速/( | 318 | 324 | 330 | 336 | 342 | 348 |
下列说法中错误的是( )
A.在这个变化过程中,当温度为10![]() 时,声速是336
时,声速是336![]()
B.温度越高,声速越快
C.当空气温度为20![]() 时,声音5
时,声音5![]() 可以传播1740
可以传播1740![]()
D.当温度每升高10![]() ,声速增加6
,声速增加6![]()





