Question

【题目】若能分解成两个一次因式的积，则整数k=_________.

Answer 1

【答案】

【解析】

根据题意设多项式可以分解为：（x+ay+c）（2x+by+d），则2c+d=k，根据cd=6，求出所有符合条件的c、d的值，然后再代入ad+bc=0求出a、b的值，与2a+b=1联立求出a、b的值，a、b是整数则符合，否则不符合，最后把符合条件的值代入k进行计算即可．

解：设能分解成：(x＋ay＋c)（2x＋by＋d)，

即2x2+aby2＋（2a＋b）xy＋（2c＋d)x＋（ad＋bc)y＋cd，

∴cd=6，

∵6=1×6=2×3=（-2）×（-3）=(-1)×(-6)，

∴①c=1，d=6时，ad＋bc=6a＋b=0，与2a＋b=1联立求解得，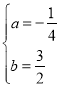

或c=6，d=1时，ad＋bc=a＋6b=0,与2a＋b=1联立求解得，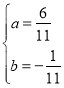

②c=2，d=3时，ad＋bc=3a＋2b=0，与2a＋b=1联立求解得，

或c=3，d=2时，ad＋bc=2a＋3b=0，与2a＋b=1联立求解得,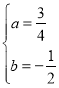

③c=-2，d=-3时，ad＋bc=-3a-2b=0，与2a＋b=1联立求解得，

或c=-3，d=-2，ad＋bc=-2a-3b=0，与2a＋b=1联立求解得，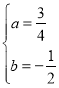

④c=-1，d=-6时，ad＋bc=-6a-b=0，与2a＋b=1联立求解得，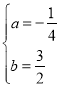

或c=-6，d=-1时，ad＋bc=-a-6b=0，与2a＋b=1联立求解得，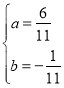

∴c=2，d=3时，c=-2，d=-3时，符合，

∴k=2c＋d=2×2＋3=7，k=2c＋d=2×（-2）＋（-3)=-7，

∴整数k的值是7，-7．

故答案为：．