题目内容

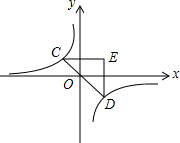
如图，已知四边形AOBE和四边形CBFD均为正方形，反比例函数y=
4
x
的图象经过D、E两点，则△DOE的面积等于（　　）
A．
6
-1		B．
5
2
C．2D．
6

设正方形CBFD的边长为x，
正方形AOBE，且反比例函数y=
4
x
的图象经过点E，易得E的坐标为（2，2）；
故点D的坐标可表示为（x，2+x）；
又有反比例函数y=
4
x
的图象经过D，
则x•（2+x）=4，解可得x=
5
-1；
则AE=OA=2，BC=BF=
5
-1，EF=3-
5
，
则S△DOE=S正方形AOBE+S正方形AOBE+S△DEF-S△OCD-S△OAE=2；
故选C．
练习册系列答案
相关题目
如图，已知反比例函数y=
k
x
（k＞0）的图象经过点A（2，m），过点A作AB⊥x轴于点B，且S△AOB=3．若一次函数y=ax+1的图象经过点A，并且与x轴相交于点C，求AO：AC的值．
如图所示，P是反比例函数y=
k
x
图象上一点，过P分别向x轴、y轴引垂线，若S阴=3，则解析式为______．
已知双曲线y=
k
x
经过点（-1，3），如果A（a1，b1），B（a2，b2）两点在该双曲线上，且a1＜a2＜0，那么b1______b2．
如图，已知点C为反比例函数y=-
6
x
上的一点，连结C0并延长交双曲线的另一个分支于D点，过C点向y轴引垂线，过D点向x轴引垂线，两直线相交于E点，那么△CDE的面积为______．
点P，Q在y=-
3
x
的图象上．
（1）若P（1，a），Q（2，b），比较a，b的大小；
（2）若P（-1，a），Q（-2，b），比较a，b的大小；
（3）你能从中发现y随x增大时的变化规律吗？
（4）若P（x1，y1），Q（x2，y2），x1＜x2，你能比较y1与y2的大小吗？
反比例数y=
k
x
的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果S△MON=2，则k的值为______．
如图，函数y1=
k1
x
与y2=k2x的图象相交于点A（1，2）和点B，当y1＜y2时，自变量x的取值范围是（　　）
A．x＞1B．-1＜x＜0
C．-1＜x＜0或x＞1D．x＜-1或0＜x＜1
如图，直线x=t（t＞0）与反比例函数y=
2
x
，y=-
1
x
的图象分别交于B，C两点，A为y轴上的任意一点，则△ABC的面积为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网