题目内容
【题目】如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足 ![]() +(b2﹣16)2=0.
+(b2﹣16)2=0. 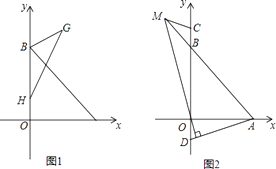
(1)求A、B两点的坐标,∠OAB的度数;
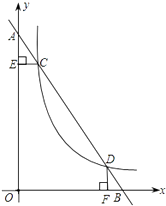
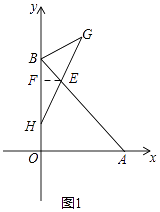
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,
①求点E到BH的距离;
②求点G的坐标;
(3)如图2,C,D是y轴上两点,且BC=OD,连接AD,过点O作MN⊥AD于点N,交直线AB于点M,连接CM,求∠ADO+∠BCM的值.
【答案】
(1)解:∵ ![]() +(b2﹣16)2=0,
+(b2﹣16)2=0,
∴a﹣b=0,b2﹣16=0,
解得:b=4,a=4或b=﹣4,a=﹣4,
∵A点在x轴正半轴,B点在y轴正半轴上,
∴b=4,a=4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠OAB=45°
(2)解:①如图1,作EF⊥y轴于F,
∵B(0,4),H(0,1),
∴BH=OB﹣OH=4﹣1=3,
∵OA=OB=4,
∴△OAB为等腰直角三角形,
∴∠OBA=∠OAB=45°,
∴△BFE为等腰直角三角形,
∴BF=EF=2,
∴OF=OB﹣BF=4﹣1=3,
∴E(2,3),
∴E(2,3)为GH的中点,
∵S△BHE=3,
∴ ![]() BH×EF=3,即
BH×EF=3,即 ![]() ×3×EF=3,
×3×EF=3,
∴EF=2,
故点E到BH的距离为2.
②设G(m,n),则
∵BE为△BHG的中线,
∴ ![]() ,
, ![]() ,
,
解得m=4,n=5,
∴G点坐标为(4,5)
(3)解:如图2,过点B作BK⊥OC,交MN于点K,则∠KBO=∠DOA,
∵MN⊥AD,
∴∠DON+∠NOA=90°,
∴∠3+∠NOA=90°,
∵∠NOA+∠1=90°,
∴∠3=∠1,
在△KOB和△OAD中,
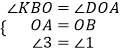 ,
,
∴△KOB≌△OAD(ASA),
∴KB=OD,∠2=∠7,
∵BC=OD,
∴KB=BC,
∵OB=OA,∠BOA=90°,
∴∠OBA=45°,
∴∠9=∠8=45°,
在△MKB和△MCB中,
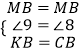 ,
,
∴△MKB≌△MCB(SAS),
∴∠6=∠5,
∵∠7+∠6=180°,
∴∠2+∠5=180°,即∠ADO+∠BCM=180°.
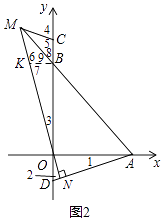
【解析】(1)根据非负数的性质,得出关于a、b的方程组,求得a、b即可得到A、B两点的坐标,最后利用等腰三角形的性质得出∠OAB的度数;(2)作EF⊥y轴于F,构造等腰直角三角形BEF,进而求出E点坐标,利用△BHE的面积即可得到点E到BH的距离;设G(m,n),根据BE为△BHG的中线,求得点G坐标即可;(3)过点B作BK⊥OC,交MN于点K,然后证明△OBK≌△OAD、△MKB≌△MCB,从而可证明∠ADO+∠BCM=180°.
【考点精析】掌握等腰直角三角形和三角形的面积是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;三角形的面积=1/2×底×高.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案